
���� �٣���������P��x0��y0��б�ʲ����ڵ�ֱ�߲������÷���y-y0=k��x-x0����ʾ��
�ڣ���x1��x2ʱ����б�ʴ��ڿ����÷��̣�y-y1����x2-x1��=��x-x1����y2-y1������ʾ����x1=x2ʱ��ֱ�߷���Ϊx=x1�������÷��̣�y-y1����x2-x1��=��x-x1����y2-y1������ʾ��
�ۣ���ֱ�߹�ԭ��ʱ��ֱ�߲������÷���$\frac{x}{a}$+$\frac{y}{b}$=1��ʾ��
�ܣ�������Q��0��b����ֱ�ߣ���б�ʲ�����ʱ�������Ա�ʾΪy=kx+b��
��� �⣺���ڢ٣���������P��x0��y0��б�ʲ����ڵ�ֱ�߲������÷���y-y0=k��x-x0����ʾ���ʢ���ȷ��
���ڢڣ�����������ͬ�ĵ�P1��x1��y1����P2��x2��y2����ֱ���������������x1��x2ʱ����б�ʴ��ڿ����÷��̣�y-y1����x2-x1��=��x-x1����y2-y1������ʾ����x1=x2ʱ��ֱ�߷���Ϊx=x1�������÷��̣�y-y1����x2-x1��=��x-x1����y2-y1������ʾ���ʢ���ȷ��
���ڢۣ���ֱ�߹�ԭ��ʱ��ֱ�߲������÷���$\frac{x}{a}$+$\frac{y}{b}$=1��ʾ���ʢ���ȷ��
���ڢܣ�������Q��0��b����ֱ�ߣ���б�ʲ�����ʱ�������Ա�ʾΪy=kx+b���ʢܴ���
�ʴ�Ϊ���ܣ�
���� ���⿼����������ٵ��ж����漰����ֱ�߷��̵ı���ʽ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|0��x��1} | B�� | {x|-1��x��2} | C�� | {x|-1��x��2} | D�� | {x|0��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{1}{2}$ | B�� | $\frac{1}{2}$ | C�� | -2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� | 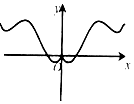 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com