分析:(1)设AB
1的中点为P,连接NP、MP.根据三角形△AB
1B中PN是中位线,以及矩形BB
1C
1C中M是CC
1中点,可证明出CM∥NP且CM=NP,从而四边形CNPM是平行四边形,可得CN∥MP,根据线面平行的判定定理,得到CN∥平面AMB
1.
(2)根据正三棱柱的性质,结合线面垂直的判定和性质,可得B
1M⊥AG.设AC=2a,结合题中
CC1=AC和线面垂直的位置关系,算出MG
2+B
1M
2=
B1G2,得出B
1M⊥MG.最后根据线面垂直的判定定理,得到B
1M⊥平面AMG.
(3)根据AG⊥平面BGM,得AG是三棱锥A-B
1GM的高.算出△B
1GM的面积并结合棱锥体积公式,可得三棱锥A-B
1GM的体积,得到V
AMB1G=V
A-B1GM=
a
3,而易得三棱柱ABC-A
1B
1C
1的体积V=
S△ABC×CC1=2a3,由此不难算出四面体AMB
1G与三棱柱ABC-A
1B
1C
1的体积之比.
解答:解:(1)设AB
1的中点为P,连接NP、MP…(1分)
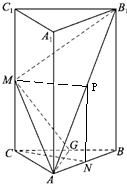
∵△AB
1B中,PN是中位线,∴PN∥B
1B且PN=
B
1B
又∵矩形BB
1C
1C中,CM∥B
1B且CM=
B
1B
∴CM∥NP且CM=NP…(2分)
∴四边形CNPM是平行四边形,可得CN∥MP…(3分)
∵CN?平面AMB
1,MP?平面AMB
1,
∴CN∥平面AMB
1…(4分)
(2)∵CC
1⊥平面ABC,CC
1⊆平面CC
1B
1B
∴平面CC
1B
1B⊥平面ABC,
∵平面CC
1B
1B∩平面ABC=BC,AG⊥BC,∴AG⊥平面CC
1B
1B,
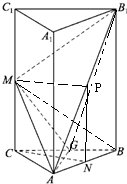
∵B
1M⊆平面CC
1B
1B,∴B
1M⊥AG.…(5分)
∵CC
1⊥平面ABC,平面A
1B
1C
1∥平面ABC,∴CC
1⊥BC,CC
1⊥B
1C
1设AC=2a,则CC
1=2
a
在Rt△MCG中,MG=
=a同理可得:B
1M=
a
∵BB
1∥CC
1,∴BB
1⊥平面ABC,可得BB
1⊥BC,
连接B
1G,可得B
1G=
=3a,
∴MG
2+B
1M
2=
B1G2,∴B
1M⊥MG,…(7分)
又AG∩MG=G,∴B
1M⊥平面AMG..…(8分)
(3)结合(2)中所设数据,可得
VABC-A1B1C1=S△ABC•CC1=2a3…(9分)
∵AG⊥平面BGM,∴AG是三棱锥A-B
1GM的高
∵S
△B1GM=
GM×MB
1=
×
a×
a=
a
2,
∴三棱锥A-B
1GM的体积V
A-B1GM=
×S
△B1GM×AG=
×
a
2×
a=
a
3,
即V
AMB1G=V
A-B1GM=
a
3,…(10分)
∴
VAMB1G:VABC-A1B1C1=1:4…(12分)
点评:本题给出特殊三棱柱,求证线面垂直、线面平行并求多面体的体积之比,着重考查了空间线面平行的判定、线面垂直的判定与性质和锥体、柱体的体积公式等知识,属于中档题.

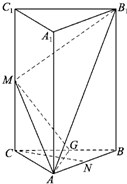 (2012•赣州模拟)如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=
(2012•赣州模拟)如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=



 (2012•赣州模拟)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为
(2012•赣州模拟)如图放置的边长为1的正方形PABC沿x轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为