
【题目】执行下面的程序框图,如果输入的t=0.01,则输出的n=( ) 
A.5
B.6
C.7
D.8
【答案】C
【解析】解:第一次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=1,不满足退出循环的条件; 再次执行循环体后,S=
,n=1,不满足退出循环的条件; 再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=2,不满足退出循环的条件;
,n=2,不满足退出循环的条件;
再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=3,不满足退出循环的条件;
,n=3,不满足退出循环的条件;
再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=4,不满足退出循环的条件;
,n=4,不满足退出循环的条件;
再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=5,不满足退出循环的条件;
,n=5,不满足退出循环的条件;
再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=6,不满足退出循环的条件;
,n=6,不满足退出循环的条件;
再次执行循环体后,S= ![]() ,m=
,m= ![]() ,n=7,满足退出循环的条件;
,n=7,满足退出循环的条件;
故输出的n值为7,
故选:C
【考点精析】利用程序框图对题目进行判断即可得到答案,需要熟知程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标![]() )、推理(能力指标
)、推理(能力指标![]() )、建模(能力指标
)、建模(能力指标![]() )的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养;若
的值评定学生的数学核心素养;若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为![]() ,从数学核心素养等级不是一级的学生中任取一人,其综合指标为
,从数学核心素养等级不是一级的学生中任取一人,其综合指标为![]() ,记随机变量
,记随机变量![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形PABC的各边及对角线长度都相等,D、E、F、G分别是AB、BC、CA、AP的中点,下列四个结论中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC.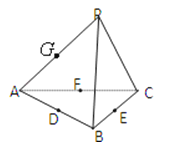
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AC⊥BC,E、F分别在线段B1C1和AC上,B1E=3EC1 , AC=BC=CC1=4
(1)求证:BC⊥AC1;
(2)试探究满足EF∥平面A1ABB1的点F的位置,并给出证明.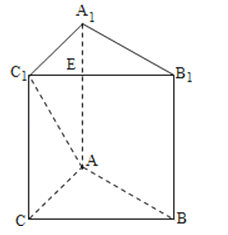
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在实数集
在实数集![]() 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数![]() 存在常数
存在常数![]() 使得
使得![]() 恒成立,则称
恒成立,则称![]() 是一个“关于
是一个“关于![]() 函数”.现有下列“关于
函数”.现有下列“关于![]() 函数”的结论:
函数”的结论:
①常数函数是“关于![]() 函数”;
函数”;
②正比例函数必是一个“关于![]() 函数”;
函数”;
③“关于![]() 函数”至少有一个零点;
函数”至少有一个零点;
④![]() 是一个“关于
是一个“关于![]() 函数”.
函数”.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,点![]() (n∈N*)均在函数y=3x-2的图象上.
(n∈N*)均在函数y=3x-2的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com