Question

【题目】空间四边形PABC的各边及对角线长度都相等，D、E、F、G分别是AB、BC、CA、AP的中点，下列四个结论中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC．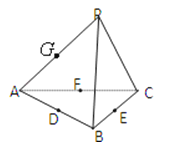

Answer 1

【答案】①②
【解析】解：∵空间四边形PABC的各边及对角线长度都相等，
D、E、F、G分别是AB、BC、CA、AP的中点，
∴BC∥DF，又BC不包含于平面PDF，DF平面PDF，
∴BC∥平面PDF，故①正确；
∵DE⊥BC，AE⊥BC，DE∩AE=E，
∴BC⊥平面PAE，
∵DF∥BC，∴DF⊥平面PAE，故②正确；
∵DG∥PB，GF∥PC，DG∩GF=G，DG，GF平面GDF，
∴平面GDF∥平面PBC，故③正确；
∵BC⊥平面PAE，BC平面ABC，
∴平面PAE⊥平面ABC，故④正确．
所以答案是：①②③④．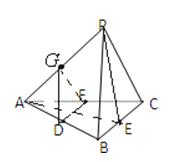

【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案，需要熟知平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．