
已知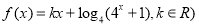 是偶函数.
是偶函数.
(1)求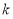 的值;
的值;
(2)证明:对任意实数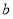 ,函数
,函数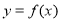 的图像与直线
的图像与直线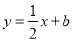 最多只有一个交点;
最多只有一个交点;
(3)设 若函数
若函数 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数 的取值范围.
的取值范围.
(1)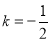 ;(2)证明见解析;(3)
;(2)证明见解析;(3)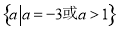 .
.
【解析】
试题分析:(1)由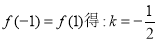 ,并进行检验;(2)原问题等价于证明方程组
,并进行检验;(2)原问题等价于证明方程组
 最多只有一组解,即证方程
最多只有一组解,即证方程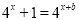 最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程:
最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程: 只有唯一解,令
只有唯一解,令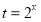 ,则可化为关于
,则可化为关于 的方程:
的方程: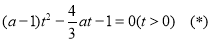 只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数
只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数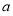 的取值范围.
的取值范围.
试题解析:【解析】
(1)由 经检验的
经检验的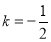 满足题意; 2分
满足题意; 2分
(2)证明:即证方程组 最多只有一组解,
最多只有一组解,
即证方程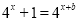 最多只有一个实根. 4分
最多只有一个实根. 4分
下面用反证法证明:
假设上述方程有两个不同的解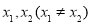 则有:
则有:
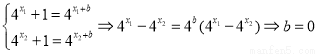 .
.
但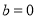 时,
时,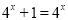 不成立.
不成立.
故假设不成立.从而结论成立. 7分
(3)问题转化为方程: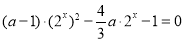 只有唯一解. 9分
只有唯一解. 9分
令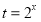 ,则可化为关于
,则可化为关于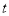 的方程:
的方程: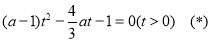 只有唯一正根. 10分
只有唯一正根. 10分
若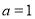 ,则上述方程变为
,则上述方程变为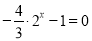 ,无解.故
,无解.故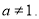 11分
11分
若二次方程(*)两根异号,即 .此时方程(*)有唯一正根,满足条件; 12分
.此时方程(*)有唯一正根,满足条件; 12分
若二次方程(*)两根相等且为正,则 . 13分
. 13分
故 的取值范围是:
的取值范围是: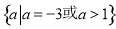 . 14分
. 14分
考点:偶函数,函数与方程,二次函数.


科目:高中数学 来源:2016届广东省高一上学期期中模块考试数学试卷(解析版) 题型:解答题
设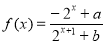 (
(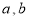 为实常数).
为实常数).
(1)当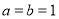 时,证明:
时,证明:
①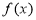 不是奇函数;②
不是奇函数;②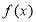 是
是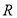 上的单调递减函数.
上的单调递减函数.
(2)设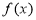 是奇函数,求
是奇函数,求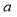 与
与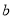 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2016届广东省高一上学期期中模块考试数学试卷(解析版) 题型:选择题
对于函数 )中任意的
)中任意的 有如下结论:
有如下结论:
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤ .
.
当 时,上述结论中正确结论的个数是( )
时,上述结论中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:高中数学 来源:2016届广东实验中学高一一级模块考试数学试卷(解析版) 题型:选择题
如图将正方形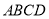 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论:

① ⊥
⊥ ;
;
②△ 是等边三角形;
是等边三角形;
③ 与
与 所成的角为60°;
所成的角为60°;
④ 与平面
与平面 所成的角为60°.
所成的角为60°.
其中错误的结论是( )
A.① B.② C.③ D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com