
【题目】对于定义在D上的函数f(x),若存在距离为d的两条直线y=kx+m1和y=kx+m2 , 使得对任意x∈D都有kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)(x∈D)有一个宽度为d的通道.给出下列函数: ①f(x)= ![]() ;
;
②f(x)=sinx;
③f(x)= ![]() ;
;
④f(x)= ![]()
其中在区间[1,+∞)上通道宽度可以为1的函数有(写出所有正确的序号).
【答案】①③④
【解析】解:函数①,在区间[1,+∞)上的值域为(0,1], 满足0≤f(x)≤1,
∴该函数在区间[1,+∞)上通道宽度可以为1;
函数②,在区间[1,+∞)上的值域为[﹣1,1],
满足﹣1≤f(x)≤1,
∴该函数在区间[1,+∞)上通道宽度可以为2;
函数③,在区间[1,+∞)上的图象是双曲线x2﹣y2=1在第一象限的部分,
其渐近线为y=x,满足x﹣1≤f(x)≤x,
∴该函数在区间[1,+∞)上通道宽度可以为1;
函数④,在区间[1,+∞)上的值域为[0, ![]() ],
],
满足0≤f(x)≤ ![]() 1,
1,
∴该函数在区间[1,+∞)上通道宽度可以为1.
故满足题意的有①③④.
所以答案是①③④.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为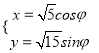 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为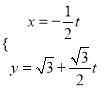 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ax2﹣3x.
(1)若a=4时,求f(x)在x∈[1,4]上的最大值和最小值;
(2)若f(x)在x∈[2,+∞]上是增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,点E,F分别为BC、PD的中点,若PA=AD=4,AB=2. 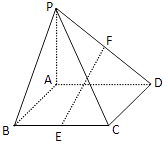
(1)求证:EF∥平面PAB.
(2)求直线EF与平面PCD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定两个命题,命题P:函数f(x)=(a﹣1)x+3在R上是增函数; 命题q:关于x的方程x2﹣x+a=0有实数根. 若p∧q为假命题,p∨q为真命题,求实数a的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
参考公式: 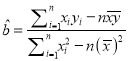 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数y= ![]() +
+ ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
③f(x)是定义在R上的奇函数,当x<0时,f(x)=2x2+x﹣1,则x≥0时,f(x)=﹣2x2+x+1
④函数y= ![]() 的值域是(﹣1,
的值域是(﹣1, ![]() ).
).
其中正确命题的序号有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com