
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
参考公式: 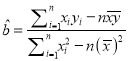 ,
, ![]() .
.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组抽出的号码为28,则第8组抽出的号码应是a;若用分层抽样方法,则50岁以下年龄段应抽取b人,那么a+b等于( ) 
A.46
B.45
C.70
D.69
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个说法: ①若向量{ ![]() 、
、 ![]() 、
、 ![]() }是空间的一个基底,则{
}是空间的一个基底,则{ ![]() +
+ ![]() 、
、 ![]() ﹣
﹣ ![]() 、
、 ![]() }也是空间的一个基底.
}也是空间的一个基底.
②空间的任意两个向量都是共面向量.
③若两条不同直线l,m的方向向量分别是 ![]() 、
、 ![]() ,则l∥m
,则l∥m ![]() ∥
∥ ![]() .
.
④若两个不同平面α,β的法向量分别是 ![]() 、
、 ![]() ,且
,且 ![]() =(1,2,﹣2)、
=(1,2,﹣2)、 ![]() =(﹣2,﹣4,4),则α∥β.
=(﹣2,﹣4,4),则α∥β.
其中正确的说法的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在D上的函数f(x),若存在距离为d的两条直线y=kx+m1和y=kx+m2 , 使得对任意x∈D都有kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)(x∈D)有一个宽度为d的通道.给出下列函数: ①f(x)= ![]() ;
;
②f(x)=sinx;
③f(x)= ![]() ;
;
④f(x)= ![]()
其中在区间[1,+∞)上通道宽度可以为1的函数有(写出所有正确的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y恒有f(x)=f(y)+f(x﹣y),当x>0时,f(x)<0,且f(2)=﹣3.
(1)求f(0),并判断函数f(x)的奇偶性;
(2)证明:函数f(x)在R上的单调递减;
(3)若不等式f(2x﹣3)﹣f(﹣22x)<f(k2x)+6在区间(﹣2,2)内恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=f(x)的图象向右平移 ![]() 单位得到函数y=cos2x的图象,则f(x)=( )
单位得到函数y=cos2x的图象,则f(x)=( )
A.﹣sin2x
B.cos2x
C.sin2x
D.﹣cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x≠1)
(x≠1)
(1)证明f(x)在(1,+∞)上是减函数;
(2)令g(x)=lnf(x),判断g(x)=lnf(x)的奇偶性并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com