
【题目】(本小题满分14分)
如图,四边形![]() 是正方形,△
是正方形,△![]() 与△
与△![]() 均是以
均是以![]() 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上的任意一点.
上的任意一点.
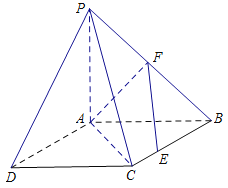
(1)求证: ![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:第(1)小题设计为证明![]() ,只需证明
,只需证明![]() 平面
平面![]() ;第(2)小题求二面角的大小,解决方法多样,既可以用综合法,也可以用向量法求解.
;第(2)小题求二面角的大小,解决方法多样,既可以用综合法,也可以用向量法求解.
试题解析:(1)证明:∵![]() 是
是![]() 的中点,且
的中点,且![]() ,∴
,∴![]() .
.
∵ △![]() 与△
与△![]() 均是以
均是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() , ∴
, ∴![]() .
.
∵ 四边形![]() 是正方形∴
是正方形∴![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
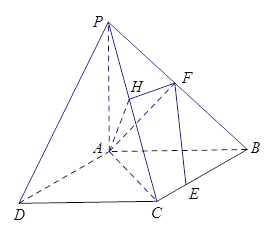
(2)解法1:作![]() 于
于![]() ,连接
,连接![]() ,
,
∵![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() ∴
∴![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ⊥平面
⊥平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∴∠![]() 为二面角
为二面角![]() 的平面角.
的平面角.
设正方形![]() 的边长为
的边长为![]() ,则
,则![]() ,
,![]() ,
,
在Rt△![]() 中,在Rt△
中,在Rt△![]() 中,
中,
![]()
![]() ,
,![]() ,
,
在Rt△![]() 中,
中,![]() .
.
所以二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .
.
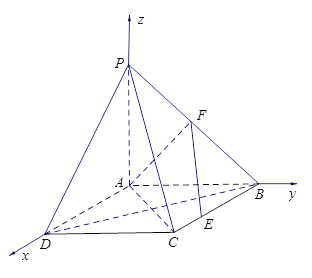
解法2:以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴 ,
轴 ,
建立空间直角坐标系![]() ,设
,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 得
得![]()
令![]() ,得
,得![]() ,∴
,∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴ 平面
,∴ 平面![]()
![]() 平面
平面![]() .
.
连接![]() ,则
,则![]() .
.
∵ 平面![]()
![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∴ 平面![]() 的一个法向量为
的一个法向量为![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
则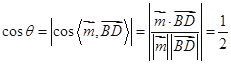 .
.
∴![]() .
.
∴ 二面角![]() 的平面角的正弦值为
的平面角的正弦值为![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
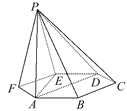
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,E,F是AD上互异的两点,G,H是BC上互异的两点,由图可知,①AB与CD互为异面直线;②FH分别与DC,DB互为异面直线;③EG与FH互为异面直线;④EG与AB互为异面直线.其中叙述正确的是 ( )
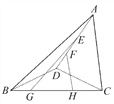
A. ①③ B. ②④ C. ①④ D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 外的直线
外的直线![]() 不平行于平面
不平行于平面![]() ,则平面
,则平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么直线
,那么直线![]() 平面
平面![]()
C. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com