
| A. | $\frac{3π}{4}$ | B. | π | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
分析 由f(x)的图象经过点P(0,$\frac{3\sqrt{2}}{2}$),且-$\frac{π}{2}$<θ<$\frac{π}{2}$,可得θ=$\frac{π}{4}$,又由g(x)的图象也经过点P(0,$\frac{3\sqrt{2}}{2}$),可求出满足条件的φ的值
解答 函数f(x)=sin(2x+θ)(-$\frac{π}{2}$<θ<$\frac{π}{2}$)向右平移φ个单位,得到g(x)=sin(2x+θ-2φ),
因为两个函数都经过P(0,$\frac{3\sqrt{2}}{2}$),
所以sinθ=$\frac{\sqrt{2}}{2}$,
又因为-$\frac{π}{2}$<θ<$\frac{π}{2}$,
所以θ=$\frac{π}{4}$,
所以g(x)=sin(2x+$\frac{π}{4}$-2φ),
sin($\frac{π}{4}$-2φ)=$\frac{\sqrt{2}}{2}$,
所以$\frac{π}{4}$-2φ=2kπ+$\frac{π}{4}$,k∈Z,此时φ=kπ,k∈Z,
或$\frac{π}{4}$-2φ=2kπ+$\frac{3π}{4}$,k∈Z,此时φ=kπ-$\frac{π}{4}$,k∈Z,
故选:C.
点评 本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,三角函数求值,难度中档


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
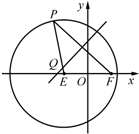 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com