考点:排列、组合的实际应用
专题:计算题,排列组合
分析:根据题意,结合四点共面的情况分3种情况讨论:①、上底面中取3个点,下底面取1个点,②、上底面中取1个点,下底面取3个点,③、上底面中取2个点,下底面取2个点,分别求出每种情况下四面体的个数,由加法原理计算可得答案.
解答:
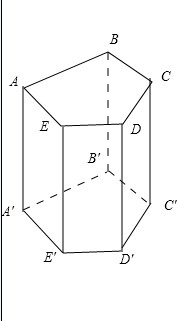
解:根据题意,如图分3种情况讨论:
①、上底面中取3个点,下底面取1个点,
共有C
53×C
51=50个四面体,
②、上底面中取1个点,下底面取3个点,
共有C
51×C
53=50个四面体,
③、上底面中取2个点,下底面取2个点,
共有C
52×C
52=100种情况,
其中共面的有3种情况:a、5个侧面,b、5个对角面,c、10个底面五边形对角线与相对底面与之平行的边确定的平面,如平面ACD′B′,
此时可以组成四面体100-5-5-10=80个;
综合可得:一个正五棱柱的顶点为顶点的四面体共有50+50+80=180个:
故答案为180.
点评:本题考查排列、组合的应用,注意4点共面包括“10个底面五边形对角线与相对底面与之平行的边确定的平面”

 解:根据题意,如图分3种情况讨论:
解:根据题意,如图分3种情况讨论:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案