
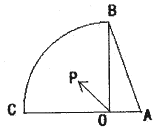
 已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1].
已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1]. 分析 以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,
表示出点A、B的坐标,得出$\overrightarrow{OP}$的坐标表示,从而求出x,y满足的约束条件,
再利用线性规划的方法求出目标函数z=x+y的最值即可得出结果.
解答 解:以OA所在直线为x轴,以OB所在直线为y轴建立平面直角坐标系,如图所示;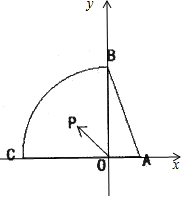
则A(1,0),B(0,2),
∴$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$=(x,0)+(0,2y)=(x,2y),
则x,y满足条件$\left\{\begin{array}{l}{-2≤x≤0}\\{0≤y≤1}\\{{x}^{2}{+4y}^{2}≤4}\end{array}\right.$,
作出可行域如图所示,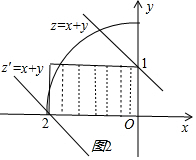
令z=x+y,化目标函数为y=-x+z,
由图可知,当直线y=-x+z过点(0,1)时,直线在y轴上的截距最大,z有最大值1;
当直线y=-x+z过点(-2,0)时,直线在y轴上的截距最小,z有最小值-2;
则x+y的取值范围是[-2,1].
故答案为:[-2,1].
点评 本题考查了简单的线性规划问题,也考查了数形结合的解题方法和转化思想,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
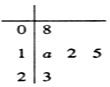 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | 14 | D. | $\frac{71}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com