
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
分析 根据题意,利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的周期性和最值,即可求出 A|x1-x2|的最小值.
解答 解:$f(x)=sin(2017x+\frac{π}{6})+cos(2017x-\frac{π}{3})$
=sin2017xcos$\frac{π}{6}$+cos2017xsin$\frac{π}{6}$+cos2017xcos$\frac{π}{3}$+sin2017xsin$\frac{π}{3}$
=$\frac{\sqrt{3}}{2}$sin2017x+$\frac{1}{2}$cos2017x+$\frac{1}{2}$cos2017x+$\frac{\sqrt{3}}{2}$sin2017x
=$\sqrt{3}$sin2017x+cos2017x
=2sin(2017x+$\frac{π}{6}$).
或$f(x)=sin(2017x+\frac{π}{6})+cos(2017x-\frac{π}{3})$
=$sin(2017x+\frac{π}{6})+cos(\frac{π}{3}-2017x)$
=2sin(2017x+$\frac{π}{6}$).
∴f(x) 的最大值为A=2;
由题意得,|x1-x2|的最小值为$\frac{T}{2}$=$\frac{π}{2017}$,
∴A|x1-x2|的最小值为$\frac{2π}{2017}$.
故选:B.
点评 本题考查了三角函数的恒等变换以及正弦、余弦函数的周期性和最值问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0} | B. | (-1,0) | C. | {-1,0} | D. | (-3,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
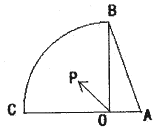 已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1].
已知在Rt△AOB中,AO=1,BO=2,如图,动点P是在以O点为圆心,OB为半径的扇形内运动(含边界)且∠BOC=90°;设$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围[-2,1].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
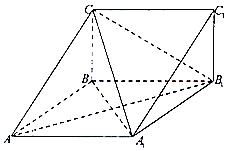 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
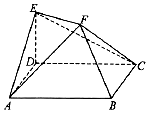 如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.
如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com