
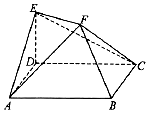
 如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.
如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.分析 (1)由ED⊥平面ABCD可得ED⊥AC,再由四边形ABCD是菱形,得BD⊥AC,然后利用线面垂直的判定可得AC⊥平面BDEF.从而得到平面EAC⊥平面BDEF;
(2)设AC∩BD=O,连结FO,由EF∥DO,且EF=DO,可得四边形EFOD是平行四边形,再由ED⊥平面ABCD,可得EO⊥DO,进一步得到AC⊥平面BDEF.
∴点A到平面BDEF的距离等于就是△ABD边BD上的高,求解直角三角形求得点A到平面BDEF的距离,再由几何体ABCDEF的体积V=VA-BDEF+VC-BDEF=2VA-BDEF求得答案.
解答 (1)证明:∵ED⊥平面ABCD,AC?平面ABCD,
∴ED⊥AC,
∵四边形ABCD是菱形,
∴BD⊥AC,
又ED∩DB=D,
∴AC⊥平面BDEF.
又AC?平面EAC,故平面EAC⊥平面BDEF;
(2)设AC∩BD=O,连结FO,∵EF∥DO,且EF=DO,
∴四边形EFOD是平行四边形,
又ED⊥平面ABCD,可得EO⊥DO,
∴四边形EFOD是矩形.
∵AC⊥平面BDEF.
∴点A到平面BDEF的距离等于就是△ABD边BD上的高,
且高$h=2sin{60°}=\sqrt{3}$.
∴几何体ABCDEF的体积V=VA-BDEF+VC-BDEF=2VA-BDEF=2×$\frac{1}{3}×\frac{1}{2}×(1+2)×\sqrt{3}=\sqrt{3}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等体积法求多面体的体积,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com