
分析 (1)已知a=1,求出函数的导数,求解f(x)的单调区间,只需令f′(x)>0解出单调增区间,令f′(x)<0解出单调减区间.
(2)区间(0,1]上的最值问题,通过导数得到单调性,结合极值点和端点的比较得到,确定待定量a的值.
解答 解:(1)当a=1时,f′(x)=$\frac{2-{x}^{2}}{x(2-x)}$,
∴当x∈(0,$\sqrt{2}$)时,f′(x)>0,
当x∈($\sqrt{2}$,2)时,f′(x)<0,
所以f(x)的单调递增区间为(0,$\sqrt{2}$),
单调递减区间为($\sqrt{2}$,2);…(5分)
(2)当x∈(0,1]时,f′(x)=$\frac{2-2x}{x(2-x)}$+a>0,
即f(x)在(0,1]上单调递增,
故f(x)在 (0,1]上的最大值为f(1)=a,
因此a=$\frac{2}{3}$.…(10分)
点评 本题考查了考查利用导数研究函数的单调性,利用导数处理函数最值等知识,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
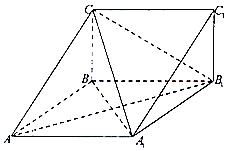 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).
某校从参加高二年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段后画出如下频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3 (结果保留一位小数).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
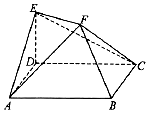 如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.
如图,ABCD是边长2的菱形,其中∠DAB=60°,ED垂直平面ABCD,ED=1,EF∥BD且2EF=BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com