练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （04年上海卷）(12分)

        已知复数z1满足(1+i)z­1=－1+5i, z­2=a－2－i, 其中i为虚数单位,a∈R, 若<,求a的取值范围.

    解析：由题意得 z1==2+3i,

      于是==,=.

      <,得a2－8a+7<0,1<a<7.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （04年上海卷）(14分)   

    记函数f(x)=的定义域为A, g(x)=lg[(x－a－1)(2a－x)](a<1) 的定义域为B.

    (1) 求A；

    (2) 若BA, 求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （04年上海卷）(16分)

    如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

    (1)     证明：P-ABC为正四面体；

    (2)     若PD=PA, 求二面角D-BC-A的大小；(结果用反三角函数值表示)

    (3)     设棱台DEF-ABC的体积为V, 是否存在体积为V且各棱长均相等的直

    平行六面体,使得它与棱台DEF-ABC有相同的棱长和? 若存在,请具体构造

    出这样的一个直平行六面体,并给出证明；若不存在,请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （04年上海卷理）(18分)

    设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点, 且a1=2, a2=2, …, an=2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.

    (1)      若C的方程为=1,n=3. 点P1(3,0) 及S3=255, 求点P3的坐标；

     (只需写出一个)

    (2)若C的方程为(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值；

    . (3)请选定一条除椭圆外的二次曲线C及C上的一点P1,对于给定的自然数n,写出符合条件的点P1, P2,…Pn存在的充要条件,并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （04年上海卷文）(本题满分14分) 第1小题满分6分, 第2小题满分8分

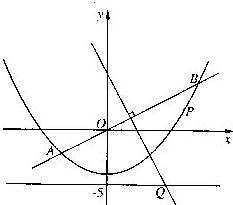
      如图, 直线y=x与抛物线y=x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

     (1) 求点Q的坐标；

    (2) 当P为抛物线上位于线段AB下方

    (含A、B) 的动点时, 求ΔOPQ面积的最大值.

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （04年上海卷文）(18分)

    设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点, 且a1=2, a2=2, …, an=2构成了一个公差为d(d≠0) 的等差数列, 其中O是坐标原点. 记Sn=a1+a2+…+an.

    (1)      若C的方程为－y2=1,n=3. 点P1(3,0) 及S3=162, 求点P3的坐标；

     (只需写出一个)

    (2)      若C的方程为y2=2px(p≠0). 点P1(0,0), 对于给定的自然数n, 证明：

    (x1+p)2, (x2+p)2, …,(xn+p)2成等差数列；

    (3)      若C的方程为(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值.

          

     

     

     

    查看答案和解析>>

    同步练习册答案