过点P(1,-2)的直线l将圆x2+y2-4x+6y-3=0截成两段弧,若其中劣弧的长度最短,那么直线l的方程为 .
【答案】
分析:过P的直线l将圆分成两条弧中,劣弧最短时,直线l与过P的直径垂直,即斜率的乘积为-1,将圆方程化为标准方程,找出圆心Q坐标,由P与Q的坐标求出直径PQ的斜率,进而求出直线l的斜率,由P坐标与求出的斜率,即可得出此时直线l的方程.
解答:解:将圆方程化为标准方程得:(x-2)
2+(y+3)
2=16,
∴圆心Q坐标为(2,-3),又P坐标为(1,-2),
∴直线QP的斜率为
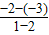
=-1,
则所求直线l的方程为y+2=x-1,即x-y-3=0.
故答案为:x-y-3=0
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,直线斜率的求法,以及直线的点斜式方程,解题的关键是明白过P的直线l将圆分成两条弧中,劣弧最短时,直线l与过P的直径垂直.

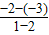 =-1,
=-1,

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案