
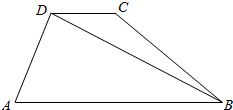
 如图,在梯形ABCD中,已知AB∥CD,∠A=60°,∠ABC=45°,AD=3cm,AB=5cm,求:BC、CD、BD.
如图,在梯形ABCD中,已知AB∥CD,∠A=60°,∠ABC=45°,AD=3cm,AB=5cm,求:BC、CD、BD. 分析 过D作DE⊥AB于E,过C作CF⊥AB于F,利用特殊角的三角函数值,即可得出结论.
解答 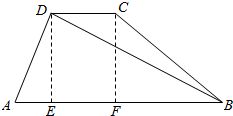 解:过D作DE⊥AB于E,过C作CF⊥AB于F.
解:过D作DE⊥AB于E,过C作CF⊥AB于F.
∵AD=3,∠DAB=60°,
∴AE=$\frac{3}{2}$,ED=$\frac{3\sqrt{3}}{2}$=CF,
∵∠ABC=45°,AB=5cm,
∴BE=$\frac{7}{2}$,BF=CF=$\frac{3\sqrt{3}}{2}$,
∴BC=$\sqrt{2}$CF=$\frac{3\sqrt{6}}{2}$,
CD=EF=BE-BF=$\frac{7-3\sqrt{3}}{2}$,BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\sqrt{19}$.
点评 本题考查三角形中线段长的求解,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
衡阳市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名后按年龄分组:第1组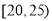 ,第2组
,第2组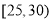 ,第3组
,第3组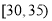 ,第4组
,第4组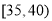 ,第5组
,第5组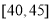 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
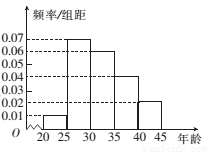
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,则应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com