考点:函数奇偶性的性质,函数奇偶性的判断
专题:函数的性质及应用
分析:首先,根据函数f(x)=a-
(a∈R)为奇函数.f(0)=0,得到a的取值,
(1)首先,求导数,然后,判断导数值的情况,从而确定单调区间;
(2)根据(1)的结论,然后,结合奇偶性,转化成恒成立问题,然后求解;
(3)构造函数h(x)=xf(x),然后,结合函数的奇偶性进行求解即可.
解答:
解:∵函数f(x)=a-
(a∈R)为奇函数,
∴f(0)=0,∴a=1.
∴f(x)=1-
,
(1)∵f'(x)=
>0,
∴函数在R上为增函数;
(2)∵f(k-2)+f(2
x+1+4
x)>0,
∴f(2
x+1+4
x)>-f(k-2)=f(2-k),
∴2
x+1+4
x>2-k,∴k>2-(2
x+1+4
x),
∵f(k-2)+f(2
x+1+4
x)>0对于任意x∈R恒成立,
∴只需k>[2-(2
x+1+4
x)]
max,
设函数g(x)=2-(2
x+1+4
x)=-(2
x)
2-2×2
x+2,
令2
x=t,(t>0),
∴g(t)=-t
2-2t+2=-(t+1)
2+3,
∴g(t)<3,∴k>3,
∴实数k的取值范围(3,+∞);
(3)设函数h(x)=xf(x)
∵函数f(x)为奇函数,
∴h(-x)=-xf(-x)=xf(x)=h(x),
∴函数h(x)=xf(x)为偶函数,
当x=0时,h(0)=0.
当x>0时,
∵2
x+1>2,
∴0<
<1,
∴1-
>0,
∴xf(x)>0,
∴当x≥0时,xf(x)≥0,
由函数图象的对称性,知函数xf(x)≥0.
点评:本题综合考查函数的单调性和奇偶性的应用,属于中档题,难度中等,注意函数为奇函数的重要性质.



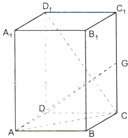 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.