考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出AD⊥平面CDD1C1,由此能够证明平面ADG⊥平面CDD1C1.
(2)当G与C1重合时,B1C1在平面ADG内;当点G与C1不重合时,B1C1∥平面ADG.利用空间几何的位置关系能够进行证明.
(3)由已知条件能够推导出∠GDC为二面角G-AD-C的平面角,由此能够求出二面角G-AD-C的大小.
解答:
(1)证明:∵ABCD-A1B1C1D1是长方体,且AB=AD,
∴AD⊥平面CDD1C1,
∵AD?平面ADG,
∴平面ADG⊥平面CDD1C1.
(2)解:当G与C1重合时,B1C1在平面ADG内,
当点G与C1不重合时,B1C1∥平面ADG.
证明:∵ABCD-A1B1C1D1是长方体,∴B1C1∥AD,
若点G与C1重合,平面ADG就是B1C1与AD确定的平面,
∴B1C1?平面ADG.
若G与C1不重合,
∵B1C1不包含于平面ADG,AD?平面ADG,且B1C1∥AD,
∴B1C1∥平面ADG.
(3)解:∵AD⊥DG,AD⊥DC,
∴∠GDC为二面角G-AD-C的平面角,
在Rt△GDC中,
∵GC=1,DC=1,
∴∠GDC=45°.
∴二面角G-AD-C的大小为45°.
点评:本题考查平面与平面垂直的证明,考查直线与平面的位置关系的判断与证明,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

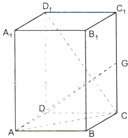 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.

 金钥匙试卷系列答案
金钥匙试卷系列答案