
【题目】函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:⑴先求出函数的定义域,再求导数![]() ,令
,令![]() ,讨论
,讨论![]() 与0的关系,从而求出函数的单调性⑵若函数
与0的关系,从而求出函数的单调性⑵若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,则必是
,则必是![]() ,得
,得![]() 、
、![]() 是
是![]() 的二根,
的二根,
∴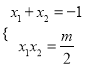 , 给出
, 给出![]() 的关系,下证
的关系,下证![]() ,构造新函数,证明不等式
,构造新函数,证明不等式
解析: ![]() 的定义域是
的定义域是![]() ,
, ![]() ,
,
(1)由题设知, ![]() ,令
,令![]() ,这是开口向上,以
,这是开口向上,以![]() 为对称轴的抛物线,
为对称轴的抛物线, ![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() ,令
,令![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
1)当![]() 即
即![]() 时,
时, ![]() ,故在
,故在![]() 上,
上, ![]() ,即
,即![]() ,在
,在![]() 上,
上, ![]() ,即
,即![]() .
.
2)当![]() 时,即
时,即![]() 时,
时,
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| + | 0 | - | 0 | + |
| 递增 | 递减 | 递增 |
综上:
![]() 时,
时, ![]() 在
在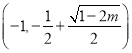 上单调递减,在
上单调递减,在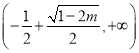 上单调递增;
上单调递增;
![]() 时,
时, ![]() 在
在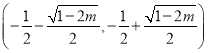 上单调递减,在
上单调递减,在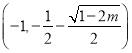 和
和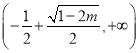 上单调递增;
上单调递增;
![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
(2)若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,
,
则必是![]() ,
, ![]() ,则
,则![]() ,
,
且![]() 在
在![]() 上单减,在
上单减,在![]() 和
和![]() 上单增,则
上单增,则![]() ,
,
∵![]() 、
、![]() 是
是![]() 的二根,
的二根,
∴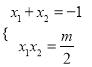 ,即
,即![]() ,
, ![]() ,
,
∴若证![]() 成立,只需证
成立,只需证
![]()
![]()
![]()
![]()
![]() .
.
即证![]()
![]() 对
对![]() 恒成立,
恒成立,
设![]()
![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
故![]() ,故
,故![]() 在
在![]() 上单增,
上单增,
故![]()
![]() ,
,
∴![]()
![]() 对
对![]() 恒成立,
恒成立,
∴![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() 都为常数),函数
都为常数),函数![]() 对应的曲线
对应的曲线![]() 、
、![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资4万元经销甲、乙两种商品,求该商场所获利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程
的极坐标方程![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,且在两坐标系中取相同的长度单位,直线
轴非负半轴建立平面直角坐标系,且在两坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为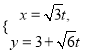 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上任意一点
上任意一点![]() 作与直线
作与直线![]() 相交的直线,该直线与直线
相交的直线,该直线与直线![]() 所成的锐角为
所成的锐角为![]() ,设交点为
,设交点为![]() ,求
,求![]() 的最大值和最小值,并求出取得最大值和最小值时点
的最大值和最小值,并求出取得最大值和最小值时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】房产税改革向前推进之路,虽历经坎坷,但步伐从未停歇,作为未来的新增税种,十二届全国人大常委会已将房产税立法正式列入五年立法规划。某市税务机关为了进一步了解民众对政府择机出台房产税的认同情况,随机抽取了一小区住户进行调查,各户人均月收入(单位:千元)的频数分布及赞成出台房产税的户数如下表:
人均月收入 |
|
|
|
|
|
|
频数 | 6 | 10 | 13 | 11 | 8 | 2 |
不赞成户数 | 5 | 9 | 12 | 9 | 4 | 1 |
若将小区人均月收入不低于7.5千元的住户称为“高收入户”,人均月收入低于7.5千元的住户称为“非高收入户”,有![]() 列联表:
列联表:
非高收入户 | 高收入户 | 总计 | |
不赞成 | |||
赞成 | |||
总计 |
(1)根据已知条件完成如图所给的![]() 列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
(2)现从月收入在![]() 的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
附:临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 的图象恰好经过第一、二、三象限的概率;
的图象恰好经过第一、二、三象限的概率;
(2)某校早上8:10开始上课,假设该校学生小张与小王在早上7:30~8:00之间到校,且每人到该时间段内到校时刻是等可能的,求两人到校时刻相差10分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com