
【题目】房产税改革向前推进之路,虽历经坎坷,但步伐从未停歇,作为未来的新增税种,十二届全国人大常委会已将房产税立法正式列入五年立法规划。某市税务机关为了进一步了解民众对政府择机出台房产税的认同情况,随机抽取了一小区住户进行调查,各户人均月收入(单位:千元)的频数分布及赞成出台房产税的户数如下表:
人均月收入 |
|
|
|
|
|
|
频数 | 6 | 10 | 13 | 11 | 8 | 2 |
不赞成户数 | 5 | 9 | 12 | 9 | 4 | 1 |
若将小区人均月收入不低于7.5千元的住户称为“高收入户”,人均月收入低于7.5千元的住户称为“非高收入户”,有![]() 列联表:
列联表:
非高收入户 | 高收入户 | 总计 | |
不赞成 | |||
赞成 | |||
总计 |
(1)根据已知条件完成如图所给的![]() 列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
(2)现从月收入在![]() 的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
附:临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.
【答案】(1)不能说明在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关; (2)![]() .
.
【解析】
(1)结合表中数据即可完成列联表,由公式![]() 求出
求出![]() 的观测者,结合表中数据即可得到答案;(2)列出所有的情况,所有的基本事件有15种,“所抽取的两户都不赞成出台房产税”包含的基本事件有10种,根据古典概型概率公式即可求出对应概率。
的观测者,结合表中数据即可得到答案;(2)列出所有的情况,所有的基本事件有15种,“所抽取的两户都不赞成出台房产税”包含的基本事件有10种,根据古典概型概率公式即可求出对应概率。
(1)由题意,可得如下![]() 列联表:
列联表:
非高收入族 | 高收入族 | 总计 | |
不赞成 | 35 | 5 | 40 |
赞成 | 5 | 5 | 10 |
总计 | 40 | 10 | 50 |
∵![]()
![]() ,
,
∴不能说明在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
(2)人均月收入在![]() 中,有5户不赞成出台房产税,分别记为
中,有5户不赞成出台房产税,分别记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;l户赞成出台房产税,记为
;l户赞成出台房产税,记为![]() .
.
现从中随机抽取两户,所有的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15个;
,共15个;
事件“所抽取的两户都不赞成出台房产税”包含的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10个,∴所抽取的两户都不赞成出台房产税的概率为
,共10个,∴所抽取的两户都不赞成出台房产税的概率为![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln2x-2aln(ex)+3,x∈[e-1,e2]
(1)当a=1时,求函数f(x)的值域;
(2)若f(x)≤-alnx+4恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对本市小学生课业负担情况进行了调查,设平均每人每天做作业的时间为![]() 分钟,有1200名小学生参加了此项调查,调查所得到的数据用程序框图处理(如图),若输出的结果是840,若用样本频率估计概率,则平均每天做作业的时间在0~60分钟内的学生的概率是( )
分钟,有1200名小学生参加了此项调查,调查所得到的数据用程序框图处理(如图),若输出的结果是840,若用样本频率估计概率,则平均每天做作业的时间在0~60分钟内的学生的概率是( )

A. 0.32 B. 0.36 C. 0.7 D. 0.84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数![]() ,其中
,其中![]() ,求函数
,求函数![]() 的图象恰好经过第一、二、三象限的概率;
的图象恰好经过第一、二、三象限的概率;
(2)某校早上8:10开始上课,假设该校学生小张与小王在早上7:30~8:00之间到校,且每人到该时间段内到校时刻是等可能的,求两人到校时刻相差10分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若平面直角坐标系内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的图象上的一个“友好点对”(点对(P,Q)与点对(Q,P)看作同一个“友好点对”).已知函数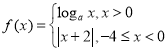
![]() ,若此函数的“友好点对”有且只有一对,则实数
,若此函数的“友好点对”有且只有一对,则实数![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 过点
过点![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设![]() ,
,![]() 是过点
是过点![]() 且关于直线
且关于直线![]() 对称的两条直线,
对称的两条直线,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点. 求证:
两点. 求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com