
【题目】关于x的不等式4x+x﹣a≤ ![]() 在x∈[0,
在x∈[0, ![]() ]上恒成立,则实数a的取值范围是( )
]上恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(0,1]
C.[﹣ ![]() ,1]
,1]
D.[1,+∞)
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】极坐标与参数方程
在直角坐标系![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).在以
为参数).在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系中,曲线
轴正半轴为极轴建立极坐标系中,曲线![]() :
: ![]() .
.
(1)当![]() ,
, ![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当![]() 时,若直线与曲
时,若直线与曲![]() 线
线![]() 相交于
相交于![]() ,
, ![]() 两点,设
两点,设![]() ,且
,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 为参数),
为参数), ![]() 是
是![]() 上的动点,且满足
上的动点,且满足![]() 为坐标原点),以原点
为坐标原点),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的普通方程;
的普通方程;
(2)利用椭圆![]() 的极坐标方程证明
的极坐标方程证明![]() 为定值,并求面积的最大值.
为定值,并求面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的平面示意图为如下图五边形区域![]() ,其中三角形区域
,其中三角形区域![]() 为生活区,四边形区域
为生活区,四边形区域![]() 为教学区,
为教学区, ![]() 为学校的主要道路(不考虑宽度).
为学校的主要道路(不考虑宽度). ![]() .
.
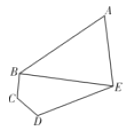
(1)求道路![]() 的长度;(2)求生活区
的长度;(2)求生活区![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com