
【题目】某学校的平面示意图为如下图五边形区域![]() ,其中三角形区域
,其中三角形区域![]() 为生活区,四边形区域
为生活区,四边形区域![]() 为教学区,
为教学区, ![]() 为学校的主要道路(不考虑宽度).
为学校的主要道路(不考虑宽度). ![]() .
.
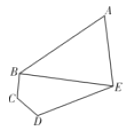
(1)求道路![]() 的长度;(2)求生活区
的长度;(2)求生活区![]() 面积的最大值.
面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】关于x的不等式4x+x﹣a≤ ![]() 在x∈[0,
在x∈[0, ![]() ]上恒成立,则实数a的取值范围是( )
]上恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(0,1]
C.[﹣ ![]() ,1]
,1]
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的连续函数g(x)满足:①当x>0时,g′(x)>0恒成立(g′(x)为函数g(x)的导函数);②对任意的x∈R都有g(x)=g(﹣x),又函数f(x)满足:对任意的x∈R,都有 ![]() 成立.当
成立.当 ![]() 时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣
时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣ ![]() ,
, ![]() ]恒成立,则a的取值范围是( )
]恒成立,则a的取值范围是( )
A.a∈R
B.0≤a≤1
C.![]()
D.a≤0或a≥1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如下数据:
手机品牌 型号 | I | II | III | IV | V |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(乙) | 5 | 7 | 9 | 4 | 3 |
手机品牌 红包个数 | 优 | 非优 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则为“非优”,请完成上述2×2列联表,据此判断是否有85%的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其他因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.
①求在型号I被选中的条件下,型号II也被选中的概率;
②以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 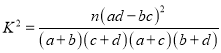 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,
, ![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() 的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为
的右焦点为F(2,0),设A、B为双曲线上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上,直线AB的斜率为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分.两人4局的得分情况如下:

(1)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求![]() 的值;
的值;
(2)如果 ![]() ,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为
,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为![]() ,求
,求![]() 的概率;
的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com