
ЎҫМвДҝЎҝјЧЎўТТБҪИЛҪшРРЙд»чұИИьЈ¬ёчЙд»ч4ҫЦЈ¬ГҝҫЦЙд»ч10ҙОЈ¬Йд»чГьЦРДҝұкөГ1·ЦЈ¬ОҙГьЦРДҝұкөГ0·ЦЈ®БҪИЛ4ҫЦөДөГ·ЦЗйҝцИзПВЈә

ЈЁ1Ј©ТСЦӘФЪТТөД4ҫЦұИИьЦРЛж»ъСЎИЎ1ҫЦКұЈ¬ҙЛҫЦөГ·ЦРЎУЪ6·ЦөДёЕВКІ»ОӘБгЈ¬ЗТФЪ4ҫЦұИИьЦРЈ¬ТТөДЖҪҫщөГ·ЦёЯУЪјЧөДЖҪҫщөГ·ЦЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©Из№ы ![]() Ј¬ҙУјЧЎўТТБҪИЛөД4ҫЦұИИьЦРЛж»ъёчСЎИЎ1ҫЦЈ¬ІўҪ«ЖдөГ·Ц·ЦұрјЗОӘ
Ј¬ҙУјЧЎўТТБҪИЛөД4ҫЦұИИьЦРЛж»ъёчСЎИЎ1ҫЦЈ¬ІўҪ«ЖдөГ·Ц·ЦұрјЗОӘ![]() Ј¬Зу
Ј¬Зу![]() өДёЕВКЈ»
өДёЕВКЈ»
ЈЁ3Ј©ФЪ4ҫЦұИИьЦРЈ¬ИфјЧЎўТТБҪИЛөДЖҪҫщөГ·ЦПаН¬Ј¬ЗТТТөД·ў»УёьОИ¶ЁЈ¬Рҙіц![]() өДЛщУРҝЙДЬИЎЦөЈ®ЈЁҪбВЫІ»ТӘЗуЦӨГчЈ©
өДЛщУРҝЙДЬИЎЦөЈ®ЈЁҪбВЫІ»ТӘЗуЦӨГчЈ©
Ўҫҙр°ёЎҝЈЁўсЈ©15Ј»ЈЁўтЈ© ![]() Ј»ЈЁўуЈ©
Ј»ЈЁўуЈ©![]() өДҝЙДЬИЎЦөОӘ
өДҝЙДЬИЎЦөОӘ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј®
Ј®
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©УЙМвТвЈ¬өГ![]() ЦРЦБЙЩУРТ»ёцІ»РЎУЪ
ЦРЦБЙЩУРТ»ёцІ»РЎУЪ![]() Ј¬УЙҙЛДЬөГөҪ
Ј¬УЙҙЛДЬөГөҪ![]() өДЦөЈ»ЈЁ2Ј©ЙиЎ°ҙУјЧТТөД
өДЦөЈ»ЈЁ2Ј©ЙиЎ°ҙУјЧТТөД![]() ҫЦұИИьЦРЛж»ъёчСЎИЎ
ҫЦұИИьЦРЛж»ъёчСЎИЎ![]() ҫЦЈ¬ЗТөГ·ЦВъЧг
ҫЦЈ¬ЗТөГ·ЦВъЧг![]() ЎұОӘКВјю
ЎұОӘКВјю![]() Ј¬јЗјЧөД
Ј¬јЗјЧөД![]() ҫЦұИИьОӘ
ҫЦұИИьОӘ![]() Ј¬ёчҫЦөДөГ·Ц·ЦұрОӘ
Ј¬ёчҫЦөДөГ·Ц·ЦұрОӘ![]() Ј»ТТҫЦөД
Ј»ТТҫЦөД![]() ҫЦұИИьОӘ
ҫЦұИИьОӘ![]() Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ
Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ![]() Ј¬АыУГБРҫЩ·ЁДЬЗуіц
Ј¬АыУГБРҫЩ·ЁДЬЗуіц![]() өДёЕВКЈ»ЈЁ3Ј©УЙМвЙиМхјюДЬЗуіц
өДёЕВКЈ»ЈЁ3Ј©УЙМвЙиМхјюДЬЗуіц![]() өДҝЙДЬөДИЎЦөОӘ
өДҝЙДЬөДИЎЦөОӘ![]() .
.
КФМвҪвОцЈәЈЁ1Ј©УЙМвТвөГ![]() Ј¬јҙ
Ј¬јҙ![]() .
.
ЎЯФЪТТөД4ҫЦұИИьЦРЛж»ъСЎИЎ1ҫЦКұЈ¬ҙЛҫЦөГ·ЦРЎУЪ6·ЦөДёЕВКІ»ОӘБгЈ¬
Ўа![]() ЦБЙЩУРТ»ёцРЎУЪ6Ј¬УЦЎЯ
ЦБЙЩУРТ»ёцРЎУЪ6Ј¬УЦЎЯ![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬
Ј¬
Ўа![]() Ј¬Ўа
Ј¬Ўа![]() .
.
ЈЁ2Ј©ЙиЎ°ҙУјЧЎўТТөД4ҫЦұИИьЦРЛж»ъёчСЎИЎ1ҫЦЈ¬ЗТөГ·ЦВъЧг![]() ЎұОӘКВјю
ЎұОӘКВјю![]() Ј¬
Ј¬
јЗјЧөД4ҫЦұИИьОӘ![]() Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ6,6,9,9Ј»ТТөД4ҫЦұИИьОӘ
Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ6,6,9,9Ј»ТТөД4ҫЦұИИьОӘ![]() Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ7,9,6,10.ФтҙУјЧЎўТТөД4ҫЦұИИьЦРЛж»ъёчСЎИЎ1ҫЦЈ¬ЛщУРҝЙДЬөДҪб№ыУР16ЦЦЈ¬ЛьГЗКЗЈә
Ј¬ёчҫЦөДөГ·Ц·ЦұрКЗ7,9,6,10.ФтҙУјЧЎўТТөД4ҫЦұИИьЦРЛж»ъёчСЎИЎ1ҫЦЈ¬ЛщУРҝЙДЬөДҪб№ыУР16ЦЦЈ¬ЛьГЗКЗЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .¶шКВјю
.¶шКВјю![]() өДҪб№ыУР8ЦЦЈ¬ЛьГЗКЗЈә
өДҪб№ыУР8ЦЦЈ¬ЛьГЗКЗЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ЎаКВјю
Ј¬ЎаКВјю![]() өДёЕВК
өДёЕВК![]() .
.
ЈЁ3Ј©![]() өДЛщУРҝЙДЬИЎЦөОӘ6Ј¬7Ј¬8.
өДЛщУРҝЙДЬИЎЦөОӘ6Ј¬7Ј¬8.


 ҝЪЛгДЬКЦПөБРҙр°ё
ҝЪЛгДЬКЦПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТӘК№gЈЁxЈ©=3x+1+tөДНјПуІ»ҫӯ№эөЪ¶юПуПЮЈ¬ФтtөДИЎЦө·¶О§ОӘЈЁ Ј©
A.tЎЬ©Ғ1
B.tЈј©Ғ1
C.tЎЬ©Ғ3
D.tЎЭ©Ғ3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝijѧУөДЖҪГжКҫТвНјОӘИзПВНјОеұЯРОЗшУт![]() Ј¬ЖдЦРИэҪЗРОЗшУт
Ј¬ЖдЦРИэҪЗРОЗшУт![]() ОӘЙъ»оЗшЈ¬ЛДұЯРОЗшУт
ОӘЙъ»оЗшЈ¬ЛДұЯРОЗшУт![]() ОӘҪМС§ЗшЈ¬
ОӘҪМС§ЗшЈ¬ ![]() ОӘѧУөДЦчТӘөАВ·ЈЁІ»ҝјВЗҝн¶ИЈ©.
ОӘѧУөДЦчТӘөАВ·ЈЁІ»ҝјВЗҝн¶ИЈ©. ![]() .
.
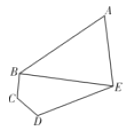
ЈЁ1Ј©ЗуөАВ·![]() өДіӨ¶ИЈ»ЈЁ2Ј©ЗуЙъ»оЗш
өДіӨ¶ИЈ»ЈЁ2Ј©ЗуЙъ»оЗш![]() Гж»эөДЧоҙуЦөЈ®
Гж»эөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЦРС§ЙъОпРЛИӨРЎЧйФЪѧУЙъОпФ°өШЦЦЦІБЛТ»ЕъГы№уКчГзЈ¬ОӘБЛБЛҪвКчГзЙъіӨЗйҝцЈ¬ҙУХвЕъКчГзЦРЛж»ъөШІвБҝБЛЖдЦР50ҝГКчГзөДёЯ¶ИЈЁөҘО»ЈәАеГЧЈ©.°СХвР©ёЯ¶ИБРіЙБЛИзПВөДЖөВК·ЦІјұнЈә

ЈЁ1Ј©ФЪХвЕъКчГзЦРИОИЎТ»ҝГЈ¬ЖдёЯ¶ИІ»өНУЪ80АеГЧөДёЕВКҙуФјКЗ¶аЙЩЈҝ
ЈЁ2Ј©ХвЕъКчГзөДЖҪҫщёЯ¶ИҙуФјКЗ¶аЙЩЈҝЈЁУГёчЧйөДЦРјдЦөҙъМжёчЧйКэҫЭөДЖҪҫщЦөЈ©
ЈЁ3Ј©ОӘБЛҪшТ»ІҪ»сөГСРҫҝЧКБПЈ¬ИфҙУ![]() ЧйЦРТЖіцТ»ҝГКчГзЈ¬ҙУ
ЧйЦРТЖіцТ»ҝГКчГзЈ¬ҙУ![]() ЧйЦРТЖіцБҪҝГКчГзҪшРРКФСйСРҫҝЈ¬Фт
ЧйЦРТЖіцБҪҝГКчГзҪшРРКФСйСРҫҝЈ¬Фт![]() ЧйЦРөДКчГз
ЧйЦРөДКчГз![]() әН
әН![]() ЧйЦРөДКчГз
ЧйЦРөДКчГз![]() Н¬Кұұ»ТЖіцөДёЕВККЗ¶аЙЩЈҝ
Н¬Кұұ»ТЖіцөДёЕВККЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ЁТеУтУлЦөУт¶јКЗ[©Ғ2Ј¬2]өДБҪёцәҜКэfЈЁxЈ©ЎўgЈЁxЈ©өДНјПуИзНјЛщКҫЈЁКөПЯІҝ·ЦЈ©Ј¬ФтПВБРЛДёцГьМвЦРЈ¬
ўЩ·ҪіМf[gЈЁxЈ©]=0УР6ёцІ»Н¬өДКөКэёщЈ»
ўЪ·ҪіМg[fЈЁxЈ©]=0УР4ёцІ»Н¬өДКөКэёщЈ»
ўЫ·ҪіМf[fЈЁxЈ©]=0УР5ёцІ»Н¬өДКөКэёщЈ»
ўЬ·ҪіМg[gЈЁxЈ©]=0УР3ёцІ»Н¬өДКөКэёщЈ»
ХэИ·өДГьМвКЗЈЁ Ј©
A.ўЪўЫўЬ
B.ўЩўЬ
C.ўЪўЫ
D.ўЩўЪўЫўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі·юЧ°і§ЙъІъТ»ЦЦ·юЧ°Ј¬Гҝјю·юЧ°өДіЙұҫОӘ40ФӘЈ¬іці§өҘјЫ¶ЁОӘ60ФӘЈ¬ёГі§ОӘ№ДАшПъКЫЙМ¶©№әЈ¬ҫц¶ЁөұТ»ҙО¶©№әБҝі¬№э100јюКұЈ¬Гҝ¶а¶©№әТ»јюЈ¬¶©№әөДИ«Іҝ·юЧ°өДіціЎөҘјЫҫНҪөөН0.02ФӘЈ¬ёщҫЭКРіЎөчІйЈ¬ПъКЫЙМТ»ҙО¶©№әБҝІ»»бі¬№э600јюЈ®
ЈЁ1Ј©ЙиТ»ҙО¶©№әxјюЈ¬·юЧ°өДКөјКіці§өҘјЫОӘpФӘЈ¬РҙіцәҜКэp=fЈЁxЈ©өДұнҙпКҪЈ»
ЈЁ2Ј©өұПъКЫЙМТ»ҙО¶©№ә¶аЙЩјю·юЧ°КұЈ¬ёГі§»сөГөДАыИуЧоҙуЈҝЖдЧоҙуАыИуКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ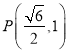 ОӘНЦФІ
ОӘНЦФІ![]() ЙПөДөгЈ¬ЗТ
ЙПөДөгЈ¬ЗТ![]() Ј¬№эөг
Ј¬№эөг![]() өД¶ҜЦұПЯУлФІ
өД¶ҜЦұПЯУлФІ![]() ПаҪ»УЪ
ПаҪ»УЪ![]() БҪөгЈ¬№эөг
БҪөгЈ¬№эөг![]() ЧчЦұПЯ
ЧчЦұПЯ![]() өДҙ№ПЯУлНЦФІ
өДҙ№ПЯУлНЦФІ![]() ПаҪ»УЪөг
ПаҪ»УЪөг![]() Ј®
Ј®
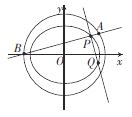
ЈЁ1Ј©ЗуНЦФІ![]() өДАлРДВКЈ»
өДАлРДВКЈ»
ЈЁ2Ј©Иф![]() Ј¬Зу
Ј¬Зу![]() Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬РЎ»ӘәНРЎГчБҪёцРЎ»п°йФЪТ»ЖрЧцУОП·Ј¬ЛыГЗНЁ№э»®ИӯЈЁјфө¶ЎўКҜН·ЎўІјЈ©ұИИьҫцКӨЛӯКЧПИөЗЙПөЪ3ёцМЁҪЧЈ¬ЛыГЗ№ж¶ЁҙУЖҪөШҝӘКјЈ¬ГҝҙО»®ИӯУ®өДТ»·ҪөЗЙПТ»ј¶МЁҪЧЈ¬КдөДТ»·ҪФӯөШІ»¶ҜЈ¬ЖҪҫЦКұБҪёцИЛ¶јЙПТ»ј¶МЁҪЧЈ¬Из№ыТ»·ҪБ¬РшБҪҙОУ®Ј¬ДЗГҙЛыҪ«¶оНв»сөГТ»ҙОЙПТ»ј¶МЁҪЧөДҪұАшЈ¬іэ·ЗТСҫӯөЗЙПөЪ3ёцМЁҪЧЈ¬өұУРИОәОТ»·ҪөЗЙПөЪ3ёцМЁҪЧКұЈ¬УОП·ҪбКшЈ¬јЗҙЛКұБҪёцРЎ»п°й»®ИӯөДҙОКэОӘ![]() Ј®
Ј®

ЈЁ1Ј©ЗуУОП·ҪбКшКұРЎ»ӘФЪөЪ2ёцМЁҪЧөДёЕВКЈ»
ЈЁ2Ј©Зу![]() өД·ЦІјБРәНКэС§ЖЪНыЈ®
өД·ЦІјБРәНКэС§ЖЪНыЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©= ![]() Ј¬Фт№ШУЪәҜКэFЈЁxЈ©=fЈЁfЈЁxЈ©Ј©өДБгөгёцКэЈ¬ХэИ·өДҪбВЫКЗ Ј® ЈЁРҙіцДгИПОӘХэИ·өДЛщУРҪбВЫөДРтәЕЈ©
Ј¬Фт№ШУЪәҜКэFЈЁxЈ©=fЈЁfЈЁxЈ©Ј©өДБгөгёцКэЈ¬ХэИ·өДҪбВЫКЗ Ј® ЈЁРҙіцДгИПОӘХэИ·өДЛщУРҪбВЫөДРтәЕЈ©
ўЩk=0КұЈ¬FЈЁxЈ©ЗЎУРТ»ёцБгөгЈ®ўЪkЈј0КұЈ¬FЈЁxЈ©ЗЎУР2ёцБгөгЈ®
ўЫkЈҫ0КұЈ¬FЈЁxЈ©ЗЎУР3ёцБгөгЈ®ўЬkЈҫ0КұЈ¬FЈЁxЈ©ЗЎУР4ёцБгөгЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com