
【题目】如图,小华和小明两个小伙伴在一起做游戏,他们通过划拳(剪刀、石头、布)比赛决胜谁首先登上第3个台阶,他们规定从平地开始,每次划拳赢的一方登上一级台阶,输的一方原地不动,平局时两个人都上一级台阶,如果一方连续两次赢,那么他将额外获得一次上一级台阶的奖励,除非已经登上第3个台阶,当有任何一方登上第3个台阶时,游戏结束,记此时两个小伙伴划拳的次数为![]() .
.

(1)求游戏结束时小华在第2个台阶的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据等可能性知每次赢、平、输的概率皆为![]() .再分两种情况分别计数:一种是小华在第1个台阶,并且小明在第2个台阶,最后一次划拳小华平;另一种是小华在第2个台阶,并且小明也在第2个台阶,最后一次划拳小华输,逆推确定事件数及对应划拳的次数,最后利用互斥事件概率加法公式求概率,(2)先确定随机变量取法,再分别利用组合求对应概率,列表可得分布列,最后根据数学期望公式求期望.
.再分两种情况分别计数:一种是小华在第1个台阶,并且小明在第2个台阶,最后一次划拳小华平;另一种是小华在第2个台阶,并且小明也在第2个台阶,最后一次划拳小华输,逆推确定事件数及对应划拳的次数,最后利用互斥事件概率加法公式求概率,(2)先确定随机变量取法,再分别利用组合求对应概率,列表可得分布列,最后根据数学期望公式求期望.
试题解析:解:(1)易知对于每次划拳比赛基本事件共有![]() 个,其中小华赢(或输)包含三个基本事件上,他们平局也为三个基本事件,不妨设事件“第
个,其中小华赢(或输)包含三个基本事件上,他们平局也为三个基本事件,不妨设事件“第![]() 次划拳小华赢”为
次划拳小华赢”为![]() ;事件“第
;事件“第![]() 次划拳小华平”为
次划拳小华平”为![]() ;事件“第
;事件“第![]() 次划拳小华输”为
次划拳小华输”为![]() ,所以
,所以![]() .
.
因为游戏结束时小华在第2个台阶,所以这包含两种可能的情况:
第一种:小华在第1个台阶,并且小明在第2个台阶,最后一次划拳小华平;
其概率为![]() ,
,
第二种:小华在第2个台阶,并且小明也在第2个台阶,最后一次划拳小华输,
其概率为![]()
所以游戏结束时小华在第2个台阶的概率为![]() .
.
(2)依题可知![]() 的可能取值为2、3、4、5,
的可能取值为2、3、4、5,
![]() ,
,
![]() ,
,
![]()
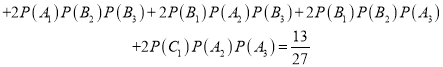
![]() ,
,
所以![]() 的分布列为:
的分布列为:
| 2 | 3 | 4 | 5 |
|
|
|
|
|
所以![]() 的数学期望为:
的数学期望为:
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的连续函数g(x)满足:①当x>0时,g′(x)>0恒成立(g′(x)为函数g(x)的导函数);②对任意的x∈R都有g(x)=g(﹣x),又函数f(x)满足:对任意的x∈R,都有 ![]() 成立.当
成立.当 ![]() 时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣
时,f(x)=x3﹣3x.若关于x的不等式g[f(x)]≤g(a2﹣a+2)对x∈[﹣ ![]() ,
, ![]() ]恒成立,则a的取值范围是( )
]恒成立,则a的取值范围是( )
A.a∈R
B.0≤a≤1
C.![]()
D.a≤0或a≥1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分.两人4局的得分情况如下:

(1)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求![]() 的值;
的值;
(2)如果 ![]() ,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为
,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为![]() ,求
,求![]() 的概率;
的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园, 公园形状为直角梯形QPRE(其中线段EQ和RP为两条底边).记QP=x(km),公园面积为S(km2).
(Ⅰ)以A为坐标原点,AE所在直线为x轴建立平面直角坐标系,求AF所在抛物线的标准方程;
(Ⅱ)求面积S(km2)关于x(km)的函数解析式;
(Ⅲ)求面积S(km2)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l:y=k(x+1)(k≠0)与椭圆3x2+y2=a2(a>0)相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点. (Ⅰ)证明:a2> ![]() ;
;
(Ⅱ)若 ![]() ,求△OAB的面积取得最大值时的椭圆方程.
,求△OAB的面积取得最大值时的椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(1)求通项an;
(2)若bn=log2an , 数列{bn}的前n项和为Sn , 且Sn=360,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com