
【题目】已知函数f(x)= ![]() ,则关于函数F(x)=f(f(x))的零点个数,正确的结论是 . (写出你认为正确的所有结论的序号)
,则关于函数F(x)=f(f(x))的零点个数,正确的结论是 . (写出你认为正确的所有结论的序号)
①k=0时,F(x)恰有一个零点.②k<0时,F(x)恰有2个零点.
③k>0时,F(x)恰有3个零点.④k>0时,F(x)恰有4个零点.
【答案】②④
【解析】解:
①当k=0时,f(x)= ![]() ,当x≤0时,f(x)=1,则f(f(x))=f(1)=
,当x≤0时,f(x)=1,则f(f(x))=f(1)= ![]() =0,
=0,
此时有无穷多个零点,故①错误;
②当k<0时,(Ⅰ)当x≤0时,f(x)=kx+1≥1,
此时f(f(x))=f(kx+1)= ![]() ,令f(f(x))=0,可得:x=0;
,令f(f(x))=0,可得:x=0;
(Ⅱ)当0<x≤1时, ![]() ,此时
,此时
f(f(x))=f( ![]() )=
)= ![]() ,令f(f(x))=0,可得:x=
,令f(f(x))=0,可得:x= ![]() ,满足;
,满足;
(Ⅲ)当x>1时, ![]() ,此时f(f(x))=f(
,此时f(f(x))=f( ![]() )=k
)=k ![]() +1>0,此时无零点.
+1>0,此时无零点.
综上可得,当k<0时,函数有两零点,故②正确;
③当k>0时,(Ⅰ)当x≤ ![]() 时,kx+1≤0,此时f(f(x))=f(kx+1)=k(kx+1)+1,
时,kx+1≤0,此时f(f(x))=f(kx+1)=k(kx+1)+1,
令f(f(x))=0,可得: ![]() ,满足;
,满足;
(Ⅱ)当 ![]() 时,kx+1>0,此时f(f(x))=f(kx+1)=
时,kx+1>0,此时f(f(x))=f(kx+1)= ![]() ,令f(f(x))=0,可得:x=0,满足;
,令f(f(x))=0,可得:x=0,满足;
(Ⅲ)当0<x≤1时, ![]() ,此时f(f(x))=f(
,此时f(f(x))=f( ![]() )=
)= ![]() ,令f(f(x))=0,可得:x=
,令f(f(x))=0,可得:x= ![]() ,满足;
,满足;
(Ⅳ)当x>1时, ![]() ,此时f(f(x))=f(
,此时f(f(x))=f( ![]() )=k
)=k ![]() +1,令f(f(x))=0得:x=
+1,令f(f(x))=0得:x= ![]() >1,满足;
>1,满足;
综上可得:当k>0时,函数有4个零点.故③错误,④正确.
所以答案是:②④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分.两人4局的得分情况如下:

(1)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求![]() 的值;
的值;
(2)如果 ![]() ,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为
,从甲、乙两人的4局比赛中随机各选取1局,并将其得分分别记为![]() ,求
,求![]() 的概率;
的概率;
(3)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l:y=k(x+1)(k≠0)与椭圆3x2+y2=a2(a>0)相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点. (Ⅰ)证明:a2> ![]() ;
;
(Ⅱ)若 ![]() ,求△OAB的面积取得最大值时的椭圆方程.
,求△OAB的面积取得最大值时的椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点为极点,
为倾斜角),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位,曲线
轴正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和参数方程;
的普通方程和参数方程;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求线段
两点,求线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,
两点, ![]() ,点
,点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() 为等腰直角三角形,记
为等腰直角三角形,记 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售量8万件.
(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?
(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 ![]() (x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入
(x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入 ![]() x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(1)求通项an;
(2)若bn=log2an , 数列{bn}的前n项和为Sn , 且Sn=360,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
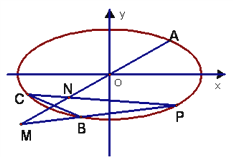
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com