练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设x，y满足x+y=20，且x，y∈R+，则lgx+lgy的最大值为（ ）
    A．40
    B．10
    C．4
    D．2
    【答案】分析：根据题意和基本不等式求出xy的范围，再由对数的运算和对数函数的单调性，求出所求的式子的最大值．
    解答：解：由题意知，x，y∈R+，x+y=20，
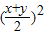
    ∴xy≤=100，当且仅当x=y时取等号，即x=y=10，
    ∴lgx+lgy=lg（xy）≤lg100=2，
    则lgx+lgy的最大值为2，
    故选D．
    点评：本题主要考查了基本不等式的应用，以及对数的运算和对数函数的单调性，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设x，y满足
    x+y≤0
    x2+y2≤2
    ，则x+2y的最大值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足
    x+y≤4
    x-2y≤-1
    x≥1
    ，则z=2x+y    的最大值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足
    x-y≥0
    x+y≤1
    x+2y≥1
    ，则目标函数z=2x+y的最大值为
    2
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足
    x+y≤4
    x-2y≤-1
    x≥1
    ，则z=2x+y    的最大值为
    19
    3
    19
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y满足
    x+y≤1
    y≤x
    y≥0
    ，则z=3x+y的最大值是
    3
    3
    ．

    查看答案和解析>>

    同步练习册答案