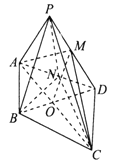
【题目】在四棱锥
中，四边形
为平行四边形， 
， 
， 
， 
为
的中点.
（1）求证： 
平面
；
（2）求点
到平面
的距离.
【答案】(1)见解析(2) 
【解析】试题分析：
（1）连接
交
于点
，则
为
的中点，连接
.由三角形中位线的性质可得
，结合线面平行的判断定理可得
平面
.
（2）取
的中点
，连接
， 
， 
.由几何关系可证得
平面
.且
，则
.在
中，由余弦定理可得
.由勾股定理可得
，则等腰
的面积为
，设点
到平面
的距离为
，利用体积相等列方程可得点
到平面
的距离为
.
试题解析：
（1）连接
交
于点
，
则
为
的中点，连接
.
在
中， 
，
∵
平面
， 
平面
，
∴
平面
.
（2）取
的中点
，连接
， 
， 
.
∵
，∴
，
又∵
，∴
，
∴
，
∴
，
∴
，∴
平面
.
∵
， 
， 
，
∴
， 
， 
，∴
，
∴
.
在
中， 
， 
， 
，
由余弦定理，得
.
∴
，
∴
的面积为
，
设点
到平面
的距离为
.
∵
，
∴
，∴
.
即点
到平面
的距离为
.
科目：高中数学 来源： 题型：
【题目】甲乙两地相距
海里，某货轮匀速行驶从甲地运输货物到乙地，运输成本包括燃料费用和其他费用．已知该货轮每小时的燃料费与其速度的平方成正比，比例系数为
，其他费用为每小时
元，且该货轮的最大航行速度为
海里/小时．
（
）请将该货轮从甲地到乙地的运输成本
表示为航行速度
（海里/小时）的函数．
（
）要使从甲地到乙地的运输成本最少，该货轮应以多大的航行速度行驶？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系中，曲线
： 
经过伸缩变换
后得到曲线
.以坐标原点
为极点， 
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（Ⅰ）求出曲线
、
的参数方程；
（Ⅱ）若
、
分别是曲线
、
上的动点，求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正方形ABCD中，E、F分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF把这个正方形折成一个空间图形，使B、C、D三点重合，重合后的点记为H，那么，在这个空间图形中必有（ ）
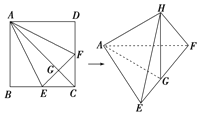
A. 
所在平面B. 
所在平面
C. 
所在平面D. 
所在平面
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲乙两名运动员互不影响地进行四次设计训练，根据以往的数据统计，他们设计成绩均不低于8环（成绩环数以整数计），且甲乙射击成绩（环数）的分布列如下：
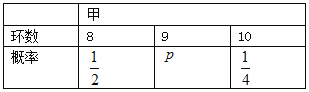
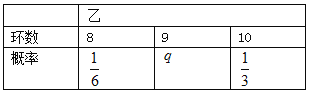
（I）求
， 
的值；
（II）若甲乙两射手各射击两次，求四次射击中恰有三次命中9环的概率；
（III）若两个射手各射击1次，记两人所得环数的差的绝对值为
，求
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
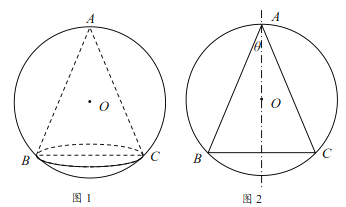
【题目】某艺术品公司欲生产一款迎新春工艺礼品，该礼品是由玻璃球面和该球的内接圆锥组成，圆锥的侧面用于艺术装饰，如图1.为了便于设计，可将该礼品看成是由圆
及其内接等腰三角形
绕底边
上的高所在直线
旋转180°而成，如图2.已知圆的半径为
，设
，圆锥的侧面积为
.
（1）求
关于
的函数关系式；
（2）为了达到最佳观赏效果，要求圆锥的侧面积最大.求取得最大值时腰
的长度.
查看答案和解析>>
科目：高中数学 来源： 题型：
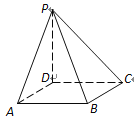
【题目】在四棱锥P–ABCD中，底面ABCD是边长为6的正方形，PD平面ABCD，PD=8．
(1) 求PB与平面ABCD所成角的大小；
(2) 求异面直线PB与DC所成角的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
