
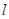 �����Ȳ��ƣ����е�ΪM�����Ѹõؿ��Ϊ�����֣����Ե�OΪ����ԭ�㣬���߶�OC����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ�����ر�AE���㺯��
�����Ȳ��ƣ����е�ΪM�����Ѹõؿ��Ϊ�����֣����Ե�OΪ����ԭ�㣬���߶�OC����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ�����ر�AE���㺯�� ����ͼ���ҵ�M����OA����Ϊ
����ͼ���ҵ�M����OA����Ϊ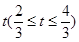 ��
�� ʱ����ֱ·
ʱ����ֱ·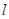 ���ڵ�ֱ�߷��̣�
���ڵ�ֱ�߷��̣�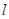 ����Ӿ���Dz�����ȡ��������ֵ�Ƕ��٣�
����Ӿ���Dz�����ȡ��������ֵ�Ƕ��٣�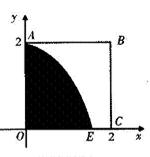
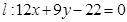 ��2��
��2��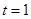 ��
��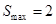
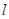 ��ر�AE���У��е�ΪM����M����OA����Ϊ
��ر�AE���У��е�ΪM����M����OA����Ϊ �����
�����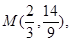 ������б��Ϊ
������б��Ϊ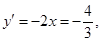 �����߷���Ϊ
�����߷���Ϊ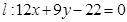 ����2����t��ʾ���ؿ�OABC��ֱ·
����2����t��ʾ���ؿ�OABC��ֱ·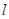 ����Ӿ���Dz�����.
����Ӿ���Dz�����. 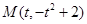 �����е�M������
�����е�M������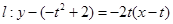 ��
��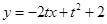 ����
����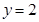 ��
��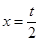 ��������
��������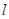 ��AB���ڵ�
��AB���ڵ�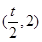 ��
��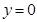 ����
���� ����
���� ��
��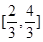 �ݼ�������
�ݼ�������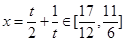 ,������
,������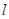 ��OC���ڵ�
��OC���ڵ�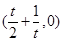 ,�ؿ�OABC������
,�ؿ�OABC������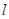 ���ϲ�������Ϊֱ�����Σ����
���ϲ�������Ϊֱ�����Σ����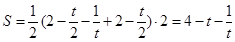
 ���Ⱥ�
���Ⱥ�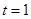 ��
��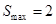 .
.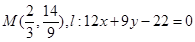 6��
6��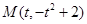 �����е�M������
�����е�M������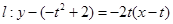
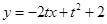 ����
����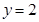 ��
��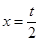 ��������
��������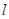 ��AB���ڵ�
��AB���ڵ�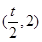 ��
��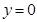 ����
���� ����
���� ��
��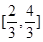 �ݼ�������
�ݼ�������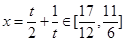
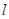 ��OC���ڵ�
��OC���ڵ�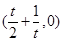 ��
�� �ؿ�OABC������
�ؿ�OABC������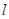 ���ϲ�������Ϊֱ�����Σ� 12��
���ϲ�������Ϊֱ�����Σ� 12��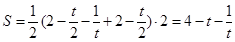
 ���Ⱥ�
���Ⱥ�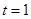 ��
��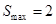 �� 16��
�� 16��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
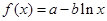 (
(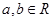 )����ͼ����
)����ͼ����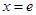 �������߷���Ϊ
�������߷���Ϊ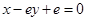 ������
������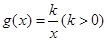 ��
��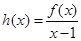 ��
��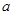 ��
��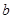 ��ֵ��
��ֵ��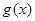 ͼ����һ��ΪԲ�ģ�2Ϊ�뾶��Բ
ͼ����һ��ΪԲ�ģ�2Ϊ�뾶��Բ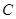 ����Բ
����Բ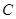 �ϴ���������ͬ�ĵ㵽ԭ��
�ϴ���������ͬ�ĵ㵽ԭ��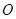 �ľ���Ϊ1����
�ľ���Ϊ1����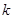 ��ȡֵ��Χ��
��ȡֵ��Χ��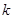 �����������
�����������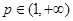 ������ʵ��
������ʵ��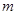 ��
��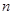 ����
����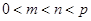 ��ʹ��
��ʹ��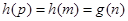 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
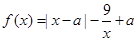 ��
��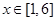 ��
��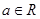 ��
��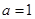 �����жϲ��ö���֤������
�����жϲ��ö���֤������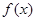 �ĵ����ԣ�
�ĵ����ԣ�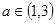 ʱ����֤����
ʱ����֤����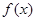 ���ڷ�������
���ڷ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��(���ޣ�2) | B��(0,3) | C��(1,4) | D��(2������) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
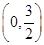 ʱ��f(x)��ln(x2��x��1)������f(x)������[0,6]�ϵ�������Ϊ(����)
ʱ��f(x)��ln(x2��x��1)������f(x)������[0,6]�ϵ�������Ϊ(����)| A��3 | B��5 | C��7 | D��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
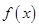 ��������
�������� ��
��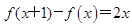 .
.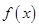 ��
��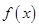 ������
������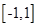 �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
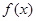 ��
��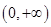 �ϵ����ݼ���
�ϵ����ݼ���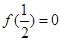 ��
��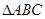 ���ڽ�A����
���ڽ�A����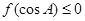 ����A��ȡֵ��Χ�ǣ� ��
����A��ȡֵ��Χ�ǣ� ��A��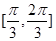 | B��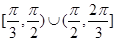 | C��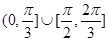 | D��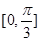 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��a����1 | B��|a|��1 | C��|a|��1 | D��a��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com