
【题目】已知函数f(x)在(0, ![]() )上处处可导,若[f(x)﹣f′(x)]tanx﹣f(x)<0,则( )
)上处处可导,若[f(x)﹣f′(x)]tanx﹣f(x)<0,则( )
A.![]() 一定小于
一定小于 ![]()
B.![]() 一定大于
一定大于 ![]()
C.![]() 可能大于
可能大于 ![]()
D.![]() 可能等于
可能等于 ![]()
【答案】A
【解析】解:∵[f(x)﹣f′(x)]tanx﹣f(x)<0,∴f(x)sinx<f′(x)sinx+f(x)cosx.
令g(x)=f(x)sinx,则g′(x)=f′(x)sinx+f(x)cosx>f(x)sinx=g(x).∴g′(x)﹣g(x)>0.
令h(x)= ![]() ,则h′(x)=
,则h′(x)= ![]() >0.∴h(x)是增函数.
>0.∴h(x)是增函数.
∴h(ln ![]() )<h(ln
)<h(ln ![]() ),即
),即 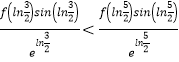 ,化简得f(ln
,化简得f(ln ![]() )sin(ln
)sin(ln ![]() )<0.6f(ln
)<0.6f(ln ![]() )sin(ln
)sin(ln ![]() ).
).
故选:A.
构造g(x)=f(x)sinx,根据已知条件判断g(x)与g′(x)的关系,再构造h(x)= ![]() ,判断h(x)的单调性,利用单调性得出结论.
,判断h(x)的单调性,利用单调性得出结论.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a=1时,求函数f(x)在[1,e]上的最小值和最大值;
(2)当a≤0时,讨论函数f(x)的单调性;
(3)是否存在实数a,对任意的x1,x2![]() (0,+∞),且x1≠x2,都有
(0,+∞),且x1≠x2,都有![]() 恒成立.若存在,求出a的取值范围;若不存在,说明理由.
恒成立.若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50﹣90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)≤0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升”,在该问题中第3天共分发大米( )
A. 192升 B. 213升 C. 234升 D. 255升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线于A,B两点,若点P的纵坐标是m(m≠0),点D为准线l与x轴的交点.

(1)若m=2,求△DAB的面积;
(2)设![]() =λ
=λ![]() =μ
=μ![]() ,求证:λ+μ为定值.
,求证:λ+μ为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“t≠0,mt=ntm=n”类比得到“c≠0,a·c=b·ca=b”;
④“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑤“(m·n)t=m(n·t)”类比得到“(a·b)·c=a(b·c)”;
⑥“![]() ”类比得到
”类比得到![]() .以上的式子中,类比得到的结论正确的是________.
.以上的式子中,类比得到的结论正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是[40,50)和[90,100]的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com