
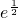 +
+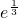 +…+
+…+ ≥ln(n+1)+n(n∈N*).
≥ln(n+1)+n(n∈N*).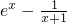
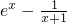 ,则g′(x)=
,则g′(x)=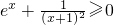
 ,则
,则 ≥ln(
≥ln( +1)+1=ln(n+1)-lnn+1
+1)+1=ln(n+1)-lnn+1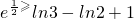 ,…,
,…, ≥ln(n+1)-lnn+1
≥ln(n+1)-lnn+1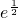 +
+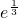 +…+
+…+ ≥ln(n+1)+n(n∈N*).
≥ln(n+1)+n(n∈N*).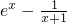 ,构建新函数g(x)=
,构建新函数g(x)=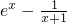 ,从而可得函数f(x)在[0,+∞)上单调递增,即可求出f(x)在该区间上的最小值;
,从而可得函数f(x)在[0,+∞)上单调递增,即可求出f(x)在该区间上的最小值; ,可得
,可得 ≥ln(n+1)-lnn+1,再累加,即可证得结论.
≥ln(n+1)-lnn+1,再累加,即可证得结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com