
| A. | 4024 | B. | 4026 | C. | 4028 | D. | 4030 |
分析 由于$\left\{{\frac{1}{{{a_n}+{a_{n+1}}}}}\right\}$是等差数列,可得$\frac{2}{{a}_{1}(q+{q}^{2})}$=$\frac{1}{{a}_{1}(1+q)}$+$\frac{1}{{a}_{1}({q}^{2}+{q}^{3})}$,又a1=1,解得q,进而得出.
解答 解:∵$\left\{{\frac{1}{{{a_n}+{a_{n+1}}}}}\right\}$是等差数列,∴2$\frac{1}{{a}_{2}+{a}_{3}}$=$\frac{1}{{a}_{1}+{a}_{2}}$+$\frac{1}{{a}_{3}+{a}_{4}}$,即$\frac{2}{{a}_{1}(q+{q}^{2})}$=$\frac{1}{{a}_{1}(1+q)}$+$\frac{1}{{a}_{1}({q}^{2}+{q}^{3})}$,又a1=1,化为:q=1.
∴公差d=$\frac{1}{2}$-$\frac{1}{2}$=0,首项=2,
∴$(\frac{1}{a_2}+\frac{1}{a_3})+(\frac{1}{a_3}+\frac{1}{a_4})+…+(\frac{1}{{{a_{2015}}}}+\frac{1}{{{a_{2016}}}})$=2×2014=4028.
故选:C.
点评 本题考查了等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈($\frac{1}{2}$,+∞),使得x+log2x>0 | B. | ?x∈($\frac{1}{2}$,+∞),使得x+log2x≤0 | ||
| C. | ?x∈($\frac{1}{2}$,+∞),使得x+log2x≤0 | D. | ?x∈(-∞,$\frac{1}{2}$],使得x+log2x>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
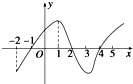 如图是y=f(x)导数的图象,对于下列四个判断:
如图是y=f(x)导数的图象,对于下列四个判断:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方体的体积与棱长的关系 | |
| B. | 学生的成绩和体重 | |
| C. | 路上酒后驾驶的人数和交通事故发生的多少 | |
| D. | 水的体积和重量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com