
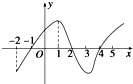
 如图是y=f(x)导数的图象,对于下列四个判断:
如图是y=f(x)导数的图象,对于下列四个判断:分析 通过图象,结合导函数的符号,根据函数单调性,极值和导数之间的关系,逐一进行判断,即可得到结论.
解答 解:由导函数的图象可得:
| x | [-2,-1) | -1 | (-1,2) | 2 | (2,4) | 4 | (4,+∞) |
| f′(x) | - | 0 | + | 0 | - | 0 | + |
| f(x) | 单减 | 极小 | 单增 | 极大 | 单减 | 极小 | 单增 |
点评 本小题考查导数的运用以及看图能力.注意看清图画的是导函数的图象,不要与函数图象混淆.考查学生的识图和应用能力.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
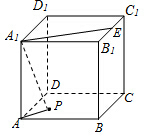 如图,棱长为2的正方形ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P在底面ABCD内,且PA1=A1E,则点P运动形成图形的长度是( )
如图,棱长为2的正方形ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P在底面ABCD内,且PA1=A1E,则点P运动形成图形的长度是( )| A. | 1 | B. | $\frac{π}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1] | C. | (1,e) | D. | ($\frac{1}{e}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4024 | B. | 4026 | C. | 4028 | D. | 4030 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{16}$ | C. | $\frac{9}{16}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| y1 | y2 | 总计 | |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 总计 | b | 46 | 100 |
| A. | 94、96 | B. | 52、54 | C. | 52、50 | D. | 54、52 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com