
分析 化简可得Tn=$\frac{3(1-{3}^{n})}{1-3}$=$\frac{3({3}^{n}-1)}{2}$,从而可化得k≥$\frac{3n-6}{\frac{{3}^{n+1}}{2}}$=$\frac{2n-4}{{3}^{n}}$,从而判断数列{$\frac{2n-4}{{3}^{n}}$}的单调性即可求数列的最大值,从而解得.
解答 解:∵${a_n}={3^n}$,
∴Tn=$\frac{3(1-{3}^{n})}{1-3}$=$\frac{3({3}^{n}-1)}{2}$,
∴Tn+$\frac{3}{2}$=$\frac{{3}^{n+1}}{2}$,
∵$({T_n}+\frac{3}{2})k≥3n-6$,
∴k≥$\frac{3n-6}{\frac{{3}^{n+1}}{2}}$=$\frac{2n-4}{{3}^{n}}$,
∵$\frac{2(n+1)-4}{{3}^{n+1}}$-$\frac{2n-4}{{3}^{n}}$=$\frac{10-4n}{{3}^{n+1}}$,
∴数列{$\frac{2n-4}{{3}^{n}}$}前3项单调递增,从第3项起单调递减,
∴当n=3时,数列{$\frac{2n-4}{{3}^{n}}$}有最大值$\frac{2}{27}$,
故$k≥\frac{2}{27}$.
故答案为:$k≥\frac{2}{27}$.
点评 本题考查了数列与不等式的综合应用,同时考查了恒成立问题与最值问题的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
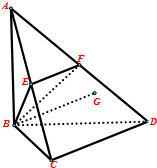 如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.
如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 196 | B. | 198 | C. | 200 | D. | 202 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
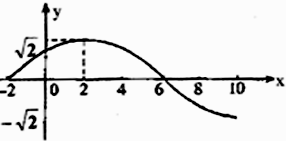 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4024 | B. | 4026 | C. | 4028 | D. | 4030 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com