
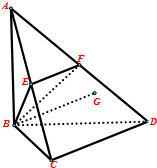
 如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.
如图:AB⊥面BCD,BC=CD,∠BCD=90°.∠ADB=30°,E,F分别是AC,AD的中点.分析 (1)要证明面面垂直,可以证明线面垂直,则过这条直线的平面与直线垂直的平面垂直.
(2)AB⊥面BCD,BCD=90°,采用补形法,利用中点的连线成中位线,平行底边即可证明.
解答 证明:(1)∵E,F分别是AC,AD的中点,∴AE=EC,AF=FD;
∴EF∥CD
又∵AB⊥面BCD,∴AB⊥CD,
$\left.\begin{array}{l}{AB⊥CD,BC⊥CD}\\{AB∩BC=B}\end{array}\right\}$⇒CD⊥平面ABC,∵$\left.\begin{array}{l}{CD⊥平面ABC}\\{EF∥CD}\end{array}\right\}$⇒EF∥平面ABC
$\left.\begin{array}{l}{EF∥平面ABC}\\{EF?平面ACD}\end{array}\right\}$⇒平面BEF⊥平面ABC
得证
解:(2)连接GD,作AB的平行线,连接AM,MD(如图所示),延长EF交MD于N.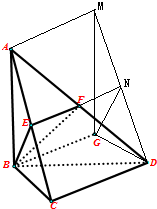 ∵E,F分别是AC,AD的中点,∴AE=EC,AF=FD;BG∥CD∥AM
∵E,F分别是AC,AD的中点,∴AE=EC,AF=FD;BG∥CD∥AM
∴EF∥CD,FN∥AM.N必为MD的中点,
∵EN∥BG,EN=BG.∴BGNE是平行四边形.
同理:BGCD是平行四边形.
∴平面BGDC∩平面BGEN=BG
∴作BG∥CD,BG是平面BEF与平面BCD的交线.证毕.
点评 本题考查了证明面面垂直,可以证明线面垂直,则过这条直线的平面与直线垂直的平面垂直.题中有中点,考虑中位线的思想.采用补形法是在解决锥体类采用方法,必须熟悉并加以运用.本题属于基础题.


科目:高中数学 来源: 题型:选择题
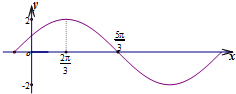
| A. | ω=1,φ=$\frac{π}{3}$ | B. | ω=1,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 012 | B. | 2 013 | C. | 2 014 | D. | 2 015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com