
分析 (1)由题意可得:${{a}_{5}}^{2}$=a2a14,可得(1+4d)2=(1+d)(1+13d),解出即可得出an,进而得到bn.
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)由题意可得:${{a}_{5}}^{2}$=a2a14,
∴(1+4d)2=(1+d)(1+13d),d>0,化为:d=2,
∴an=1+(n-1)×2=2n-1,
b2=a2=3,b3=a5=9,∴公比q=3,
∴bn=3n-1.
(2)∵数列{cn}对任意正整数n均有$\frac{{c}_{1}}{{b}_{1}}$+$\frac{c_2}{b_2}$+…+$\frac{c_n}{b_n}$=an+1成立,
∴n≥2时,$\frac{{c}_{1}}{{b}_{1}}$+$\frac{c_2}{b_2}$+…+$\frac{{c}_{n-1}}{{b}_{n-1}}$=an,∴$\frac{{c}_{n}}{{b}_{n}}$=an+1-an=2,
∴cn=2×3n.
n=1时,$\frac{{c}_{1}}{{b}_{1}}$=a2,可得c1=6.
因此?n∈N*,cn=2×3n.
∴ancn=(4n-2)×3n.
∴a1c1+a2c2+…+ancn=Tn=2×3+6×32+…+(4n-2)×3n.
3Tn=2×32+6×33+…+(4n-6)×3n+(4n-2)×3n+1,
∴-2Tn=6+4(32+33+…+3n)-(4n-2)×3n+1
=4×$\frac{3×{(3}^{n}-1)}{3-1}$-6-(4n-2)×3n+1=(4-4n)×3n+1-12,
∴Tn=6+(2n-2)×3n+1.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式、递推关系、,考查了推理能力与计算能力,属于中档题.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 012 | B. | 2 013 | C. | 2 014 | D. | 2 015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方体的体积与棱长的关系 | |
| B. | 学生的成绩和体重 | |
| C. | 路上酒后驾驶的人数和交通事故发生的多少 | |
| D. | 水的体积和重量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
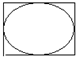 矩形长为6,宽为4,在矩形内随机地撒300粒黄豆,数得落在椭圆外的黄豆数为66颗,以此实验数据为依据可以估算出椭圆的面积为( )
矩形长为6,宽为4,在矩形内随机地撒300粒黄豆,数得落在椭圆外的黄豆数为66颗,以此实验数据为依据可以估算出椭圆的面积为( )| A. | 5.28 | B. | 16.32 | C. | 17.28 | D. | 18.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com