
【题目】已知函数![]() .
.
![]() 当
当![]() 时,试判断函数
时,试判断函数![]() 在区间
在区间![]() 上的单调性,并证明;
上的单调性,并证明;
![]() 若不等式
若不等式![]() 在
在![]() 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据函数单调性的证明的定义法,取值,做差,若![]() ,
,![]()
![]() ,判符号;(2)方法一,将问题等价于
,判符号;(2)方法一,将问题等价于![]()
![]() 恒成立,转化为轴动区间定的问题;方法二,变量分离,转化为
恒成立,转化为轴动区间定的问题;方法二,变量分离,转化为![]()
![]() 恒成立,转化为函数求最值问题.
恒成立,转化为函数求最值问题.
(1)当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增,证明如下:
上单调递增,证明如下:
对任意的![]() ,
,![]() ,若
,若![]() ,
,
![]()
![]()
![]() ,
,
由![]() ,故有:
,故有:![]() ,
,![]() ,
,
因此:![]() ,
,![]() ,
,
故有![]() 在
在![]() 上单调递增;
上单调递增;
(2)方法一:不等式![]() 在
在![]() 上恒成立
上恒成立
![]()
![]()
![]()
![]()
![]()
![]() ,
,
取![]() ,对称轴
,对称轴![]()
当![]() 时,对称轴
时,对称轴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增, ![]()
![]() ,
,
故![]() 满足题意,
满足题意,
当![]() 时,对称轴
时,对称轴![]() ,
,
又![]() 在
在![]() 上恒成立,
上恒成立,
故![]()
![]()
解得:![]() ,
,
故![]()
综上所述,实数的取值范围为![]() .
.
方法二:不等式![]() 在
在![]() 上恒成立
上恒成立
![]()
![]()
![]()
![]()
![]()
![]() 。
。
取![]()
由结论:定义在![]() 上的函数
上的函数![]() ,当且仅当
,当且仅当![]() 时
时![]() 取得最小值
取得最小值![]() .
.
故![]()
![]() 。
。
当且仅当![]() ,即
,即![]() 时函数
时函数![]() 取得最小值
取得最小值![]() .
.
故![]() ,即实数的取值范围为
,即实数的取值范围为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知AB为圆O的直径,C,D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求证:AC是∠DAB的平分线;
(2)求证:OF∥AG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图. 
(1)估计在40名广场舞者中年龄分布在[40,70)的人数;
(2)求40名广场舞者年龄的中位数和平均数的估计值;
(3)若从年龄在[20,40)中的广场舞者中任取2名,求这两名广场舞者年龄在[30,40)中的人数X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是R上的偶函数,其中e是自然对数的底数.
是R上的偶函数,其中e是自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)探究函数![]() 在
在![]() 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若函数![]() 有零点,求实数m的取值范围.
有零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,有两种方式,甲为投资债券等稳健型产品,乙为投资股票等风险型产品,设投资甲、乙两种产品的年收益分别为![]() 、
、![]() 万元,根据长期收益率市场预测,它们与投入资金
万元,根据长期收益率市场预测,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() ,
,![]() ,(其中
,(其中![]() ,
,![]() ,
,![]() 都为常数),函数
都为常数),函数![]() ,
,![]() 对应的曲线
对应的曲线![]() ,
,![]() 如图所示.
如图所示.
(1)求函数![]() 、
、![]() 的解析式;
的解析式;
(2)若该家庭现有![]() 万元资金,全部用于理财投资,问:如何分配资金能使一年的投资获得最大收益,其最大收益是多少万元?
万元资金,全部用于理财投资,问:如何分配资金能使一年的投资获得最大收益,其最大收益是多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的焦点为
)的焦点为![]() ,已知点
,已知点![]() ,
, ![]() 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足![]() .过弦
.过弦![]() 的中点
的中点![]() 作抛物线准线的垂线
作抛物线准线的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
【答案】1
【解析】设![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 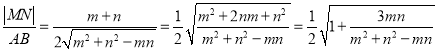
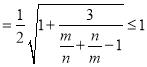 故最大值为1.
故最大值为1.
故答案为:1.
点睛:本题主要考查了抛物线的简单性质.解题的关键是利用了抛物线的定义。一般和抛物线有关的小题,很多时可以应用结论来处理的;平时练习时应多注意抛物线的结论的总结和应用。尤其和焦半径联系的题目,一般都和定义有关,实现点点距和点线距的转化。
【题型】填空题
【结束】
17
【题目】设![]() 的内角
的内角![]() ,
, ![]() ,
, ![]() 所对的边分别为
所对的边分别为![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的周长.
的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(Ⅰ)求函数![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅲ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com