
【题目】已知四棱锥![]() ,四边形
,四边形![]() 是正方形,
是正方形, ![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
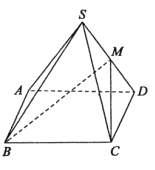
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)由![]() 可得
可得![]() ,即
,即![]() ,由
,由![]() 为正方形,可得
为正方形,可得![]() ,从而得
,从而得![]() 平面
平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)设
;(2)设![]() 的中点为
的中点为![]() ,∵
,∵![]() ,∴
,∴![]() ,面面垂直的性质可得
,面面垂直的性质可得![]() 平面
平面![]() ,在平面
,在平面![]() 内,过
内,过![]() 作直线
作直线![]() ,则
,则![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面
轴,建立空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() 为正方形,∴
为正方形,∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)
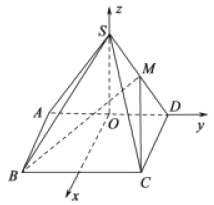
设![]() 的中点为
的中点为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
由(1)可知平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
在平面![]() 内,过
内,过![]() 作直线
作直线![]() ,则
,则![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则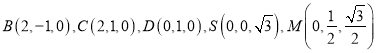 ,
,
∴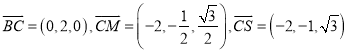 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
, 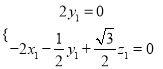 ,即
,即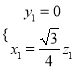 ,取
,取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
, 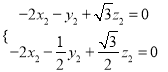 ,即
,即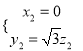 ,取
,取![]() ,
,
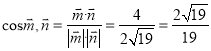 ,由图可知,二面角
,由图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查面面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() .
.
(1)已知直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)过点![]() 作直线
作直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,若弦
,若弦![]() 恰被点
恰被点![]() 平分,求直线
平分,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示. 
(1)求f(x)的解析式,并求函数f(x)在[﹣ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两俱乐部举行乒乓球团体对抗赛.双方约定:
①比赛采取五场三胜制(先赢三场的队伍获得胜利.比赛结束)
②双方各派出三名队员.前三场每位队员各比赛﹣场
已知甲俱乐部派出队员A1、A2 . A3 , 其中A3只参加第三场比赛.另外两名队员A1、A2比赛场次未定:乙俱乐部派出队员B1、B2 . B3 , 其中B1参加第一场与第五场比赛.B2参加第二场与第四场比赛.B3只参加第三场比赛
根据以往的比赛情况.甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱乐部计划以3:0取胜.则应如何安排A1、A2两名队员的出场顺序.使得取胜的概率最大?
(2)若A1参加第一场与第四场比赛,A2参加第二场与第五场比赛,各队员每场比赛的结果互不影响,设本次团体对抗赛比赛的场数为随机变量X,求X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD的对棱AD、BC成600的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
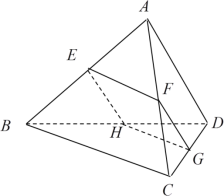
(1)求证:四边形EFGH为平行四边形;
(2)E在AB的何处时截面EFGH的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
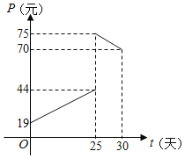
(1)请确定销售价格P(元)和时间t(天)的函数解析式;
(2)该商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)求该商品的日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com