
【题目】如图,已知![]() 所在的平面,
所在的平面, ![]() 是
是![]() 的直径,
的直径, ![]() 是
是![]() 上一点,且
上一点,且![]() 是
是![]() 中点,
中点, ![]() 为
为![]() 中点.
中点.
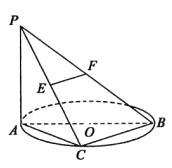
(1)求证: ![]() 面
面![]() ;
;
(2)求证: ![]() 面
面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2) 见解析(3)![]()
【解析】试题分析:(1)根据直线与平面平行的判定定理可知,只需证![]() 与面
与面![]() 内一直线平行即可,根据中位线定理可知
内一直线平行即可,根据中位线定理可知![]() ,又
,又![]() 面
面![]() 面
面![]() ,满足定理所需条件; (2)由
,满足定理所需条件; (2)由![]() 面
面![]() 面
面![]() ,则
,则![]() ,而
,而![]() 是
是![]() 的直径,则
的直径,则![]() ,又
,又![]() ,则
,则![]() 面
面![]() ,由于
,由于![]() 所以
所以![]() 面
面![]() ;(3)根据
;(3)根据![]() 面
面![]() ,则
,则![]() 即为三棱锥
即为三棱锥![]() 的高,将三棱锥
的高,将三棱锥![]() 的体积转化成三棱锥
的体积转化成三棱锥![]() 的体积,根据锥体的体积公式进行求解即可.
的体积,根据锥体的体积公式进行求解即可.
试题解析:(1)证明:在三角形![]() 中,
中, ![]() 是
是![]() 中点,
中点, ![]() 为
为![]() 中点,
中点,
∴![]() ,
, ![]() 平面
平面![]() 平面
平面![]() ,∴
,∴![]() 面
面![]() ;
;
(2)证明:∵![]() 面
面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() 是
是![]() 的直径,∴
的直径,∴![]() ,
,
又![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() ,∴
,∴![]() 面
面![]() ;
;
(3)∵![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出300人进行统计.其中对教师教学水平给出好评的学生人数为总数的60%,对教师管理水平给出好评的学生人数为总数的75%,其中对教师教学水平和教师管理水平都给出好评的有120人.
(1)填写教师教学水平和教师管理水平评价的2×2列联表:
对教师管理水平好评 | 对教师管理水平不满意 | 合计 | |
对教师教学水平好评 | |||
对教师教学水平不满意 | |||
合计 |
问:是否可以在犯错误概率不超过0.1%的前提下,认为教师教学水平好评与教师管理水平好评有关、
(2)若将频率视为概率,有4人参与了此次评价,设对教师教学水平和教师管理水平全好评的人数为随机变量X;
①求对教师教学水平和教师管理水平全好评的人数X的分布列(概率用组合数算式表示);
②求X的数学期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足: ![]() ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
(1)求数列{an},{bn}的通项公式
(2)证明:数列{bn}中的任意三项不可能成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体校为了备战明年四月份省划艇单人双桨比赛,对本校甲、乙两名划艇运动员在相同条件下进行了6次测试,测得他们划艇最大速度![]() 单位:
单位:![]() 数据如下:
数据如下:
甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
![]() 试用茎叶图表示甲、乙两名运动员测试的成绩;
试用茎叶图表示甲、乙两名运动员测试的成绩;
![]() 根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贵阳与凯里两地相距约200千米,一辆货车从贵阳匀速行驶到凯里,规定速度不得超过100千米![]() 时,已知货车每小时的运输成本
时,已知货车每小时的运输成本![]() 以元为单位
以元为单位![]() 由可变部分和固定部分组成:可变部分与速度
由可变部分和固定部分组成:可变部分与速度![]() 千米
千米![]() 时
时![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ;固定部分为64元.
;固定部分为64元.
![]() 把全程运输成本
把全程运输成本![]() 元
元![]() 表示为速度
表示为速度![]() 千米
千米![]() 时
时![]() 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
![]() 为了使全程运输成本最小,货车应以多大速度行驶?
为了使全程运输成本最小,货车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°. 
(1)求证:平面ABC1⊥平面A1B1C;
(2)设D为AC的中点,求平面ABC1与平面C1BD所成锐角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com