
【题目】如图,在直三棱柱ABC﹣A1B1C1(侧棱垂直于底面的棱柱为直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°. 
(1)求证:平面ABC1⊥平面A1B1C;
(2)设D为AC的中点,求平面ABC1与平面C1BD所成锐角的余弦值.
【答案】
(1)证明:∵直三棱柱ABC﹣A1B1C1,BC=CC1,
∴四边形BCC1B1是正方形,
∴BC1⊥B1C,
∵AB⊥BC,AB⊥BB1,BC,BB1平面BCC1B1,BC∩BB1=B,
∴AB⊥平面BCC1B1,∵BC1平面BCC1B1,
∴AB⊥BC1,又∵AB∥A1B1,
∴A1B1⊥BC1,又A1B1平面平面A1B1C,B1C平面A1B1C,A1B1∩B1C=B1,
∴BC1⊥平面A1B1C,又BC1平面ABC1,
∴平面ABC1⊥平面A1B1C.
(2)证明:∵BC=CC1=1,AC=2,∠ABC=90°.
∴AB= ![]() ,
,
建立以B为坐标原点,BC,BA,BB1分别为x,y,z轴的空间直角坐标系如图:
则B(0,0,0),C(1,0,0),B1(0,0,1),A(0, ![]() ,0),C1(1,0,1),D(
,0),C1(1,0,1),D( ![]() ,
, ![]() ,0),
,0),
设平面ABC1的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() =(1,0,1),
=(1,0,1), ![]() =(0,
=(0, ![]() ,0),
,0),
则 ![]()
![]() =x+z=0,
=x+z=0, ![]()
![]() =
= ![]() y=0,
y=0,
令x=1,则z=﹣1,y=0,即平面ABC1的法向量为, ![]() =(1,0,﹣1),
=(1,0,﹣1),
设平面C1BD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 ![]() =(1,0,1),
=(1,0,1), ![]() =(
=( ![]() ,
, ![]() ,0),
,0),
则 ![]()
![]() =x+z=0,
=x+z=0, ![]()
![]() =
= ![]() x+
x+ ![]() y=0,
y=0,
令y=1,则x=﹣ ![]() ,z=
,z= ![]() ,即平面C1BD的法向量为,
,即平面C1BD的法向量为, ![]() =(﹣
=(﹣ ![]() ,1,
,1, ![]() ),
),
则 ![]() =
= ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]()
则平面ABC1与平面C1BD所成锐角的余弦值是 ![]() .
.
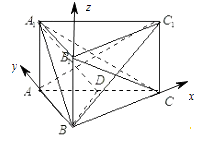
【解析】(1)由四边形BCC1B1是正方形得BC1⊥B1C,由A1B1⊥平面BCC1B1得出A1B1⊥BC1 , 故BC1⊥平面A1B1C,从而平面ABC1⊥平面A1B1C;(2)建立空间坐标系,求出平面的法向量,利用向量法即可平面ABC1与平面C1BD所成锐角的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区规划时,计划在周边建造一片扇形绿地,如图所示已知扇形绿地的半径为50米,圆心角![]() 从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与
从绿地的圆弧边界上不同于A,B的一点P处出发铺设两条道路PO与![]() 均为直线段
均为直线段![]() ,其中PC平行于绿地的边界
,其中PC平行于绿地的边界![]() 记
记![]() 其中
其中![]()

![]() 当
当![]() 时,求所需铺设的道路长:
时,求所需铺设的道路长:
![]() 若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当
若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当![]() 变化时,求铺路所需费用的最大值
变化时,求铺路所需费用的最大值![]() 精确到1元
精确到1元![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点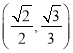 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点作斜率为
的右顶点作斜率为![]() (
(![]() )的直线交椭圆
)的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:

用广告费作解释变量,年销售额作预报变量,若认为![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型,则
的回归方程类型,则
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知商品的年利润![]() 与
与![]() 的关系式为
的关系式为![]() .根据(1)的结果,年广告费
.根据(1)的结果,年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大?
约为何值时(小数点后保留两位),年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
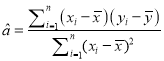 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax2+bx+1(e为自然对数的底数).
(1)若 ![]() ,求函数F(x)=f(x)ex的单调区间;
,求函数F(x)=f(x)ex的单调区间;
(2)若b=e﹣1﹣2a,方程f(x)=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|a﹣3x|﹣|2+x|.
(1)若a=2,解不等式f(x)≤3;
(2)若存在实数a,使得不等式f(x)≥1﹣a+2|2+x|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个自然数若与它的“反序数”相等,这个自然数就称为一个“魔幻数”如数“![]() ”、“
”、“![]() ”都是“魔幻数”在
”都是“魔幻数”在![]() 的元素中,去掉所有的“魔幻数”后,形成一个不含“魔幻数”的子集
的元素中,去掉所有的“魔幻数”后,形成一个不含“魔幻数”的子集![]() ,则
,则![]() 中的元素共有______个.
中的元素共有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com