练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四棱锥的底面为直角梯形，，°，底面，且，是的中点.

    （1）证明：平面平面；

    （2）求与所成角的余弦值；

    （3）求平面与平面所成二面角（锐角）的余弦值.

    【答案】（1）见解析；（2）；（3）

    【解析】

    试题（1）利用面面垂直的性质，证明CD⊥平面PAD．

    （2）建立空间直角坐标系，写出向量与的坐标，然后由向量的夹角公式求得余弦值，从而得所成角的大小.

    （3）分别求出平面的法向量和面的一个法向量，然后求出两法向量的夹角即可．

    试题解析：证明：以为坐标原点长为单位长度，如图建立空间直角坐标系，则各点坐标为.

    （1）证明：因

    由题设知，且与是平面内的两条相交直线，由此得面.又在面上，故面⊥面.

    （2）因

    （3）平面的一个法向量设为，

    平面的一个法向量设为，

    所求二面角的余弦值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在矩形中，，，为边的中点．将△沿翻折，得到四棱锥．设线段的中点为，在翻折过程中，有下列三个命题：

    ① 总有平面；

    ② 三棱锥体积的最大值为；

    ③ 存在某个位置，使与所成的角为．

    其中正确的命题是____．（写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校为增加应届毕业生就业机会，每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估，已知某年度参与评估的毕业生共有2000名，其评估成绩近似的服从正态分布．现随机抽取了100名毕业生的评估成绩作为样本，并把样本数据进行了分组，绘制了频率分布直方图：

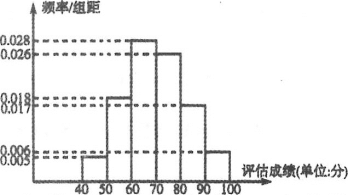
    （1）求样本平均数和样本方差（同一组中的数据用该组区间的中点值作代表）；

    （2）若学校规定评估成绩超过分的毕业生可参加三家公司的面试．

    （ⅰ）用样本平均数作为的估计值，用样本标准差作为的估计值，请利用估计值判断这2000名毕业生中，能够参加三家公司面试的人数；

    （ⅱ）若三家公司每家都提供甲、乙、丙三个岗位，岗位工资表如下：

    公司

    甲岗位

    乙岗位

    丙岗位

    9600

    6400

    5200

    9800

    7200

    5400

    10000

    6000

    5000

    李华同学取得了三个公司的面试机会，经过评估，李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为,李华准备依次从三家公司进行面试选岗，公司规定：面试成功必须当场选岗，且只有一次机会．李华在某公司选岗时，若以该岗位工资与未进行面试公司的工资期望作为抉择依据，问李华可以选择公司的哪些岗位？

    并说明理由．

    附：，若随机变量，

    则．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，真命题的个数是（　　）

    ①若“p∨q”为真命题，则“p∧q”为真命题；

    ②“a∈（0，+∞），函数y=在定义域内单调递增”的否定；

    ③l为直线，α，β为两个不同的平面，若l⊥β，α⊥β，则l∥α；

    ④“x∈R，≥0”的否定为“R，＜0”．

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥C的底面是正方形，PA⊥平面ABCD，PA=2，∠PDA=45°，点E、F分别为棱AB、PD的中点．

    （1）求证：AF∥平面PEC

    （2）求证：平面PCD⊥平面PEC；

    （3）求三棱锥C-BEP的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面ABCD为直角梯形，，，侧面底面ABCD，，．

    若PB的中点为E，求证：平面PCD；

    若，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求曲线在点处的切线方程；

    （Ⅱ）当时，求证：函数有且仅有一个零点；

    （Ⅲ）当时，写出函数的零点的个数.（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数 .

    （1）讨论函数的单调性；

    （2）若函数有两个零点，，求的取值范围，并证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，求函数的单调区间；

    （2）若恒成立，求实数的值.

    查看答案和解析>>

    同步练习册答案