
【题目】(1)由0,1,2,…,9这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种?
(2)我校高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,求不同的选取法的种数.
【答案】(1)280种;(2)472种.
【解析】
(1)千位数字和十位数字的组合有![]() 五种,百位和个位的数共有
五种,百位和个位的数共有![]() 种组合,计算得到答案.
种组合,计算得到答案.
(2)考虑不选三班的同学和选三班的一位同学两种情况,利用排除法和分步分类计数原理得到答案.
(1)十位数字与千位数字之差的绝对值等于7,
可得千位数字和十位数字的组合有![]() 五种,
五种,
每种组合中百位和个位的数共有![]() 种组合,所以符合条件的四位数共有
种组合,所以符合条件的四位数共有![]() 种.
种.
(2)情形一:不选三班的同学,从12个人中选出3人,有![]() 种选取方法,其中来自同一个班级的情况有
种选取方法,其中来自同一个班级的情况有![]() 种,则此时有
种,则此时有![]() 种选取方法;
种选取方法;
情形二:选三班的一位同学,三班的这一位同学的选取方法有4种,剩下的两位同学从剩下的12人中任选2人,有![]() 种选取方法,则此时有
种选取方法,则此时有![]() 种选取方法.
种选取方法.
根据分类计数原理,共有![]() 种选取方法.
种选取方法.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上一点,求三棱锥
上一点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() (
(![]() ),将射线
),将射线![]() 顺时针方向旋转
顺时针方向旋转![]() 得到
得到![]() :
:![]() ,且射线
,且射线![]() 与曲线
与曲线![]() 交于两点,射线
交于两点,射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+![]() )+sin(x﹣
)+sin(x﹣![]() )+cosx.
)+cosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)在△ABC中,f(A)=![]() ,△ABC的面积为
,△ABC的面积为![]() ,AB=
,AB=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
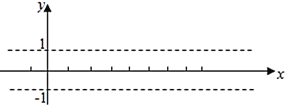
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某脐橙种植基地记录了10棵脐橙树在未使用新技术的年产量(单位:![]() )和使用了新技术后的年产量的数据变化,得到表格如下:
)和使用了新技术后的年产量的数据变化,得到表格如下:
未使用新技术的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 30 | 32 | 30 | 40 | 40 | 35 | 36 | 45 | 42 | 30 |
使用了新技术后的10棵脐橙树的年产量
第一棵 | 第二棵 | 第三棵 | 第四棵 | 第五棵 | 第六棵 | 第七棵 | 第八棵 | 第九棵 | 第十棵 | |
年产量 | 40 | 40 | 35 | 50 | 55 | 45 | 42 | 50 | 51 | 42 |
已知该基地共有20亩地,每亩地有50棵脐橙树.
(1)估计该基地使用了新技术后,平均1棵脐橙树的产量;
(2)估计该基地使用了新技术后,脐橙年总产量比未使用新技术将增产多少?
(3)由于受市场影响,导致使用新技术后脐橙的售价由原来(未使用新技术时)的每千克10元降为每千克9元,试估计该基地使用新技术后脐橙年总收入比原来增加的百分数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一本书,一碗面,一条河,一座桥”曾是兰州的城市名片,而现在“兰州马拉松”又成为了兰州的另一张名片,随着全民运动健康意识的提高,马拉松运动不仅在兰州,而且在全国各大城市逐渐兴起,参与马拉松训练与比赛的人口逐年增加.为此,某市对人们参加马拉松运动的情况进行了统计调查.其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人,对其每周参与马拉松长跑训练的天数进行统计,得到以下统计表:
平均每周进行长跑训练天数 | 不大于2天 | 3天或4天 | 不少于5天 |
人数 | 30 | 130 | 40 |
若某人平均每周进行长跑训练天数不少于5天,则称其为“热烈参与者”,否则称为“非热烈参与者”.
(1)经调查,该市约有2万人参与马拉松运动,试估计其中“热烈参与者”的人数;
(2)根据上表的数据,填写下列2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关?
热烈参与者 | 非热烈参与者 | 合计 | |
男 | 140 | ||
女 | 55 | ||
合计 |
附:k2=![]() (n为样本容量)
(n为样本容量)
P(k2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com