
【题目】如图,已知在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上一点,求三棱锥
上一点,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)要证明面面垂直,只需在一个平面内找到另一平面的一条垂线.由已知平面![]() 平面
平面![]() ,且
,且![]() ,可证
,可证![]() 平面
平面![]() ,再根据
,再根据![]() 是中位线,可证
是中位线,可证![]() ,从而
,从而![]() 平面
平面![]() ,进而再证平面
,进而再证平面![]() 平面
平面![]() ,该题实质是先找到面
,该题实质是先找到面![]() 的一条垂线
的一条垂线![]() ,再将
,再将![]() 平移到面
平移到面![]() 内;
内;
(2)点![]() 是线段
是线段![]() 的动点,考虑到
的动点,考虑到![]() 和
和![]() 到面
到面![]() 的距离相等,故
的距离相等,故![]() ,再结合第(1)问结果,取
,再结合第(1)问结果,取![]() 的中点
的中点![]() 连接
连接![]() ,据面面垂直的性质,点
,据面面垂直的性质,点![]() 到
到![]() 的距离就是三棱锥
的距离就是三棱锥![]() 的高,再求
的高,再求![]() ,进而求体积.
,进而求体积.
试题解析:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,可得
,可得![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,因此
,因此![]() 上的点
上的点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,∴
的距离,∴![]() ,取
,取![]() 的中点
的中点![]() 连接
连接![]() ,则
,则![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() ,于是
,于是![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 是正三角形,∴点
是正三角形,∴点![]() 到平面
到平面![]() 的距离等于正
的距离等于正![]() 的高,即为
的高,即为![]() ,因此,三棱锥M﹣EFG的体积
,因此,三棱锥M﹣EFG的体积![]() =
=![]() =
=![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +b(x≠0),其中a,b∈R.若对任意的a∈[
+b(x≠0),其中a,b∈R.若对任意的a∈[ ![]() ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ![]() ,1]上恒成立,则b的取值范围为明 .
,1]上恒成立,则b的取值范围为明 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
参考数据:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知命题![]() :实数
:实数![]() 满足
满足![]() ,命题
,命题![]() :实数
:实数![]() 满足方程
满足方程![]() 表示的焦点在
表示的焦点在![]() 轴上的椭圆,且
轴上的椭圆,且![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围;
的取值范围;
(2)设命题![]() :关于
:关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函数
:函数![]() 的定义域为
的定义域为![]() .若
.若![]() 是真命题,
是真命题,![]() 是假命题,求实数
是假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,BC= ![]() ,AB=AC=AA1=1,D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1 .
,AB=AC=AA1=1,D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1 . 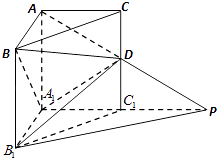
(1)求证:CD=C1D;
(2)求二面角A1﹣B1D﹣P的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点、上顶点分别为点
,右顶点、上顶点分别为点![]() ,
,
已知椭圆![]() 的焦距为
的焦距为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,当
两点,当![]() 面积取得最大时,求直线
面积取得最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+alnx(a∈R).
(1)当a=2时,求函数f(x)在点(1,f(1))处的切线方程;
(2)若函数g(x)=f(x)﹣2x+2x2 , 讨论函数g(x)的单调性;
(3)若(2)中函数g(x)有两个极值点x1 , x2(x1<x2),且不等式g(x1)≥mx2恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com