练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=x+ +b（x≠0），其中a，b∈R．若对任意的a∈[ ，2]，不等式f（x）≤10在x∈[ ，1]上恒成立，则b的取值范围为明 ．

    【答案】（﹣∞， ]
    【解析】解：∵对任意的a∈[ ，2]，不等式f（x）≤10在x∈[ ，1]上恒成立，
    ∴当a= 时，f（x）最大值为f（1）=1+ +b= +b
    当a=2时，f（x）最大值为f（ ）= +8+b= +b
    显然 +b＞ +b，
    ∴ +b≤10，
    ∴b≤ ，
    所以答案是：（﹣∞， ]
    【考点精析】利用函数单调性的性质对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点． 求证：

    （1）PA∥平面BDE；
    （2）BD⊥平面PAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知极坐标系的极点为直角坐标系xOy的原点，极轴为x轴的正半轴，两种坐标系中的长度单位相同直线的极坐标方程为，曲线C的参数方程为为参数，设直线l与曲线C交于A，B两点．

    写出直线的普通方程与曲线C的直角坐标方程；

    已知点P在曲线C上运动，求点P到直线距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某渔业公司年初用81万元购买一艘捕鱼船，第一年各种费用为1万元，以后每年都增加2万元，每年捕鱼收益30万元．

    问第几年开始获利？

    若干年后，有两种处理方案：方案一：年平均获利最大时，以46万元出售该渔船；

    方案二：总纯收入获利最大时，以10万元出售该渔船问：哪一种方案合算？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某企业生产的产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:

    质量指标值分组

    [75,85)

    [85,95)

    [95,105)

    [105,115)

    [115,125)

    频数

    6

    26

    38

    22

    8

    （1）在表格中作出这些数据的频率分布直方图;

    （2）求这些数据的众数和中位数

    （3）估计这种产品质量指标的平均数(同一组中的数据用该组区间的中点值作代表);

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在凸四边形ABCD中，AB=1，BC= ，AC⊥DC，CD= AC．设∠ABC=θ．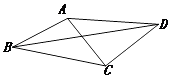

    （1）若θ=30°，求AD的长；
    （2）当θ变化时，求BD的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）在定义域[2﹣a，3]上是偶函数，在[0，3]上单调递增，并且f（﹣m2﹣ ）＞f（﹣m2+2m﹣2），则m的取值范围是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A，B，C的对边分别为a、b、c，a=btanA，且B为钝角．
    （1）证明：B﹣A= ；
    （2）求sinA+sinC的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知在四棱锥中，底面是边长为4的正方形，是正三角形，平面平面，分别是的中点.

    （1）求证：平面平面；

    （2）若是线段上一点，求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案