
分析 利用换元法,结合定积分的线性运算法则,即可求出对应的结果.
解答 解:${∫}_{-a}^{a}$x2[f(x)-f(-x)+2]dx=${∫}_{-a}^{a}$x2f(x)dx-${∫}_{-a}^{a}$x2f(-x)dx+${∫}_{-a}^{a}$2dx,
设t=-x,则dt=d(-x),
所以${∫}_{-a}^{a}$x2f(-x)dx=${∫}_{a}^{-a}$t2f(t)(-dt)=${∫}_{-a}^{a}$t2f(t)dt,
所以原式=${∫}_{-a}^{a}$x2f(x)-${∫}_{-a}^{a}$t2f(t)dt+${∫}_{-a}^{a}$2dx=2x${|}_{-a}^{a}$=4a.
故答案为:4a.
点评 本题考查了定积分的计算问题,也考查了换元法与转化思想的应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按一定的规则排成了如图所示的三角形数表(每行比上一行多一个数),设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8,若aij=2010,则i,j的值的和为( )
把正整数按一定的规则排成了如图所示的三角形数表(每行比上一行多一个数),设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8,若aij=2010,则i,j的值的和为( )| A. | 75 | B. | 76 | C. | 77 | D. | 78 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
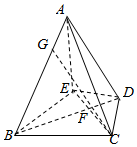 如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE,△BCE为正三角形,BD和CE的交点F,恰好平分CE,AE=BE=2,∠CDE=120°,AC=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com