
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 由题意可得S的几何意义为两点(x.lnx),(a,a)的距离的平方,求得与直线y=x平行且与曲线y=lnx相切的切点的坐标,运用点到直线的距离公式计算即可得到所求最小值.
解答 解:S=(x-a)2+(lnx-a)2(a∈R)的几何意义为:
两点(x.lnx),(a,a)的距离的平方,
由y=lnx的导数为y′=$\frac{1}{x}$,
点(a,a)在直线y=x上,
令$\frac{1}{x}$=1,可得x=1,
即有与直线y=x平行的直线且与曲线y=lnx相切的切点为(1,0),
由点到直线的距离可得d=$\frac{|1-0|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
即有S的最小值为($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$,
故选:B.
点评 本题考查最值的求法,注意运用两点的距离的几何意义,考查导数的运用:求切线的斜率,以及点到直线的距离公式,考查转化能力和运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20000元,设木工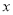 人,瓦工
人,瓦工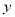 人,则工人满足的关系式是( )
人,则工人满足的关系式是( )
A.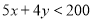 B.
B.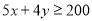
C.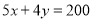 D.
D.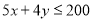
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是( )
A.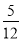 B.
B.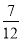 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$ | B. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$ | C. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ | D. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S15=22,d<0 | B. | S15=22,d>0 | C. | S15=15,d<0 | D. | S15=15,d>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com