
分析 (Ⅰ)求出f(x)的导数,可得切线的斜率和切点,解方程可得a的值;
(Ⅱ)求出f(x)=lnx+x,要证原不等式成立,即证xlnx+x-k(x-3)>0,可令g(x)=xlnx+x-k(x-3),求出导数,判断符号,可得单调性,即可得证;
(Ⅲ)对于在(0,1)中的任意一个常数b,假设存在正数x0,使得:${e^{f({{x_0}+1})-2{x_0}-1}}+\frac{b}{2}x_0^2<1$.运用转化思想可令H(x)=(x+1)•e-x+$\frac{b}{2}$x2-1,求出导数判断单调性,可得最小值,即可得到结论.
解答 解:(Ⅰ)函数f(x)=lnx+ax的导数为f′(x)=$\frac{1}{x}$+a,
在点(t,f(t))处切线方程为y=2x-1,
可得f′(t)=$\frac{1}{t}$+a=2,f(t)=2t-1=lnt+at,
解得a=t=1;
(Ⅱ)证明:由(Ⅰ)可得f(x)=lnx+x,
要证当x>1时,$f(x)>k({1-\frac{3}{x}})+x-1$,
即证lnx>k(1-$\frac{3}{x}$)-1(x>1),
即为xlnx+x-k(x-3)>0,
可令g(x)=xlnx+x-k(x-3),g′(x)=2+lnx-k,
由$-\frac{1}{2}≤k≤2$,x>1,可得lnx>0,2-k≥0,
即有g′(x)>0,g(x)在(1,+∞)递增,
可得g(x)>g(1)=1+2k≥0,
故当x>1时,$f(x)>k({1-\frac{3}{x}})+x-1$恒成立;
(Ⅲ)对于在(0,1)中的任意一个常数b,
假设存在正数x0,使得:${e^{f({{x_0}+1})-2{x_0}-1}}+\frac{b}{2}x_0^2<1$.
由ef(x0+1)-2x0-1+$\frac{b}{2}$x02=eln(x0+1)-x0+$\frac{b}{2}$x02=(x0+1)•e-x0+$\frac{b}{2}$x02.
即对于b∈(0,1),存在正数x0,使得(x0+1)•e-x0+$\frac{b}{2}$x02-1<0,
从而存在正数x0,使得上式成立,只需上式的最小值小于0即可.
令H(x)=(x+1)•e-x+$\frac{b}{2}$x2-1,H′(x)=e-x-(x+1)•e-x+bx=x(b-e-x),
令H′(x)>0,解得x>-lnb,令H′(x)<0,解得0<x<-lnb,
则x=-lnb为函数H(x)的极小值点,即为最小值点.
故H(x)的最小值为H(-lnb)=(-lnb+1)elnb+$\frac{b}{2}$ln2b-1=$\frac{b}{2}$ln2b-blnb+b-1,
再令G(x)=$\frac{x}{2}$ln2x-xlnx+x-1,(0<x<1),
G′(x)=$\frac{1}{2}$(ln2x+2lnx)-(1+lnx)+1=$\frac{1}{2}$ln2x>0,
则G(x)在(0,1)递增,可得G(x)<G(1)=0,则H(-lnb)<0.
故存在正数x0=-lnb,使得${e^{f({{x_0}+1})-2{x_0}-1}}+\frac{b}{2}x_0^2<1$.
点评 本题考查导数的运用:求切线的斜率、单调区间和极值、最值,考查不等式的证明,注意运用分析法和构造函数法,求得导数判断单调性,考查存在性问题的解法,注意运用转化思想和构造函数,求出导数,运用单调性,属于难题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
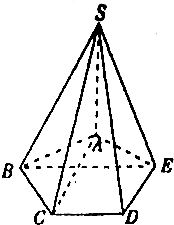 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,BC=DE=$\sqrt{3}$,∠BAE=∠BCD=∠CDE=120°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
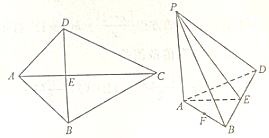 如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.
如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
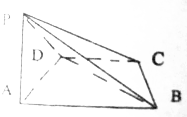 如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.
如图,在四棱锥P-ACD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB=1,PA=$\sqrt{2}$,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com