
【题目】如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,A1E=CF=1. 
(1)求两条异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值.
【答案】
(1)解:以D为原点,建立空间直角坐标系D﹣xyz如图所示:
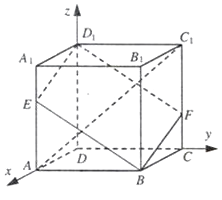
则A(3,0,0),C1=(0,3,3),D1=(0,0,3),E(3,0,2)
∴ ![]() =(﹣3,3,3),
=(﹣3,3,3), ![]() =(3,0,﹣1)
=(3,0,﹣1)
∴cosθ=  =
= ![]() =﹣
=﹣ ![]()
则两条异面直线AC1与D1E所成角的余弦值为 ![]()
(2)解:B(3,3,0), ![]() =(0,﹣3,2),
=(0,﹣3,2), ![]() =(3,0,﹣1)
=(3,0,﹣1)
设平面BED1F的一个法向量为 ![]() =(x,y,z)
=(x,y,z)
由  得
得 ![]()
令x=1,则 ![]() =(1,2,3)
=(1,2,3)
则直线AC1与平面BED1F所成角的正弦值为
| 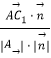 |=
|= ![]() =
= ![]()
【解析】(1)以以D为原点,建立空间直角坐标系D﹣xyz,则我们易求出已知中,各点的坐标,进而求出向量 ![]() ,
, ![]() 的坐标.代入向量夹角公式,结合异面直线夹角公式,即可得到答案.(2)设出平面BED1F的一个法向量为
的坐标.代入向量夹角公式,结合异面直线夹角公式,即可得到答案.(2)设出平面BED1F的一个法向量为 ![]() ,根据法向量与平面内任一向量垂直,数量积为0,构造方程组,求出平面BED1F的法向量为
,根据法向量与平面内任一向量垂直,数量积为0,构造方程组,求出平面BED1F的法向量为 ![]() 的坐标,代入线面夹角向量公式,即可求出答案.
的坐标,代入线面夹角向量公式,即可求出答案.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域是(0, ![]() ),f′(x)是它的导函数,且f(x)+tanxf′(x)>0在定义域内恒成立,则( )
),f′(x)是它的导函数,且f(x)+tanxf′(x)>0在定义域内恒成立,则( )
A.f( ![]() )>
)> ![]() f(
f( ![]() )
)
B.![]() sin1?f(1)>f(
sin1?f(1)>f( ![]() )
)
C.f( ![]() )>
)> ![]() f(
f( ![]() )
)
D.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数a,b,c满足a,b,c∈R+ .
(Ⅰ)若ab=1,证明:( ![]() +
+ ![]() )2≥4;
)2≥4;
(Ⅱ)若a+b+c=3,且 ![]() +
+ ![]() +
+ ![]() ≤|2x﹣1|﹣|x﹣2|+3恒成立,求x的取值范围.
≤|2x﹣1|﹣|x﹣2|+3恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.命题“若![]() ,则
,则![]() ”为假命题
”为假命题
B.命题“若![]() ,则
,则![]() ”的否命题为假命题
”的否命题为假命题
C.命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题
有实根”的逆命题为真命题
D.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(已知函数f(x)=|2x+1|+|x﹣2|,不等式f(x)≤2的解集为M.
(1)求M;
(2)记集合M的最大元素为m,若正数a,b,c满足abc=m, 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,左、右焦点分别为圆F1、F2 , M是C上一点,|MF1|=2,且|
,左、右焦点分别为圆F1、F2 , M是C上一点,|MF1|=2,且| ![]() ||
|| ![]() |=2
|=2 ![]() .
.
(1)求椭圆C的方程;
(2)当过点P(4,1)的动直线l与椭圆C相交于不同两点A、B时,线段AB上取点Q,且Q满足| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |,证明点Q总在某定直线上,并求出该定直线的方程.
|,证明点Q总在某定直线上,并求出该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线l的参数方程为 ![]() (t为参数,0<φ<π),曲线C的极坐标方程为ρcos2θ=8sinθ.
(t为参数,0<φ<π),曲线C的极坐标方程为ρcos2θ=8sinθ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当φ变化时,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。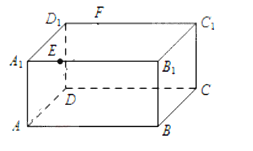
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面 把该长方体分成的两部分体积的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com