
已知非零向量a、b满足|a|=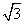 |b|,若函数f(x)=
|b|,若函数f(x)=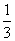 x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
A.[0, ] B.(0,
] B.(0, ]
]
C.( ,
,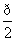 ] D.(
] D.( ,π]
,π]
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
已知首项为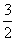 的等比数列{an}的前n项和为Sn(n∈N*), 且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*), 且-2S2,S3,4S4成等差数列.
(1)求数列{an}的通项公式;
(2) 证明Sn+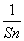 ≤
≤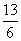 (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
给出定义:若函数f(x)在D上可导,即f ′(x)存在,且导函数f ′(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f ″(x)=(f ′(x))′.若f ″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,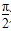 )上不是凸函数的是________(把你认为正确的序号都填上).
)上不是凸函数的是________(把你认为正确的序号都填上).
①f(x)=sinx+cosx; ②f(x)=lnx-2x;
③f(x)=-x3+2x-1; ④f(x)=xex.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)的导函数为f ′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com