
已知函数f(x)的导函数为f ′(x)=5+cosx,x∈(-1,1),且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围为________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知非零向量a、b满足|a|=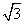 |b|,若函数f(x)=
|b|,若函数f(x)=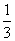 x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
A.[0, ] B.(0,
] B.(0, ]
]
C.( ,
,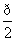 ] D.(
] D.( ,π]
,π]
查看答案和解析>>
科目:高中数学 来源: 题型:
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )
A.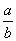 B.
B.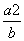 C.
C.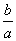 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com